Στο Διεθνές Σύστημα Μονάδων υπάρχουν επτά θεμελιώδεις μονάδες: το δευτερόλεπτο, το μέτρο, το χιλιόγραμμο, το αμπέρ, το κέλβιν, το mole και η καντέλα. Σχεδόν όλοι συμφωνούν ότι οι τέσσερις τελευταίες, αυστηρά μιλώντας, δεν είναι απαραίτητες· μπορούν να υπολογιστούν από τις τρεις πρώτες και τις χρησιμοποιούμε απλώς για ιστορικούς λόγους.
Οι τρεις που απομένουν, το δευτερόλεπτο, το μέτρο και το χιλιόγραμμο, μπορούν να εκφραστούν με τρεις θεμελιώδεις σταθερές: την ταχύτητα του φωτός, την σταθερά του Planck και κάποιο πρότυπο χρόνου – προς το παρόν την συχνότητα μιας ατομικής μετάβασης ατόμων καισίου.
1 δευτερόλεπτο (s) είναι η χρονική διάρκεια μέσα στην οποία συμβαίνουν 9.192.631.770 καθορισμένες περιοδικές ενεργειακές μεταβολές στο άτομο του καισίου (Cs133).
1 μέτρο (m) είναι η απόσταση που διανύει το φως στο κενό, στη διάρκεια 1/299.792.458 του δευτερολέπτου.
1 χιλιόγραμμο (kg) … διαβάστε ΕΔΩ: Ένα κιλό, η σταθερά του Planck και το διεθνές σύστημα μονάδων.
Η λογική είναι η εξής: από το άτομο του καισίου παίρνεις μια μονάδα μέτρησης του χρόνου. Αφού διαθέτεις μονάδα μέτρησης του χρόνου, μπορείς να χρησιμοποιήσεις την ταχύτητα του φωτός για να μετρήσεις αποστάσεις και στη συνέχεια την σταθερά του Planck για να μετρήσεις μάζες και ενέργειες. Φαίνεται λοιπόν πως χρειαζόμαστε τρεις θεμελιώδεις σταθερές. Ή μήπως όχι;
Μερικοί θεωρητικοί χορδών πιστεύουν ότι, αν βρούμε επιτέλους τη θεωρία των πάντων – κάτι που θα μπορούσε να είναι η θεωρία χορδών – τότε δεν θα πρέπει να υπάρχουν καθόλου θεμελιώδεις σταθερές. Όλα θα προκύπτουν από τα ίδια τα μαθηματικά. Άλλοι πιστεύουν ότι θα πρέπει να υπάρχει μία μόνο, η τάση της χορδής. Και κάποιοι άλλοι ότι θα είναι δύο, η τάση της χορδής και η ταχύτητα του φωτός. Οι περισσότεροι φυσικοί όμως φαίνεται να θεωρούν ότι χρειαζόμαστε τρεις θεμελιώδεις μονάδες. Λοιπόν, τι ισχύει; Καμία, μία, δύο ή τρεις;
Σε μια πρόσφατη δημοσίευσή τους στο περιοδικό Scientific Reports, οι φυσικοί Matsas et al υποστηρίζουν ότι έλυσαν το πρόβλημα. Το κατάφεραν επαναδιατυπώνοντας το ερώτημα: πόσα είδη πειραματικών οργάνων μέτρησης χρειάζονται για να περιγράψεις τα πάντα στο σύμπαν; Και η απάντησή τους είναι ότι χρειαζόμαστε μόνο ρολόγια. Αν διαθέτουμε ρολόγια, τότε μπορούμε να μετρήσουμε και αποστάσεις και μάζες, χωρίς να χρειάζεται καμία επιπλέον θεμελιώδης σταθερά πέρα από την ίδια την μονάδα του χρόνου.
Οι αποστάσεις μπορούν να μετρηθούν, εφαρμόζοντας μια πρόταση που είχε διατυπώσει πρώτος ο William Unruh: το «πείραμα με τα τρία ρολόγια». Σύμφωνα με αυτό το πείραμα, χρησιμοποιώντας την θεωρία της σχετικότητας του Αϊνστάιν μπορεί να μετρηθεί το μήκος μιας ράβδου χρησιμοποιώντας τις ενδείξεις μόνο τριών ρολογιών.
Η μέθοδος δουλεύει ως εξής: Το ρολόι Ρ1 ξεκινά από το αριστερό άκρο της ράβδου και κινείται ευθύγραμμα μέχρι το δεξί άκρο, με κάποια άγνωστη σταθερή ταχύτητα. Ο μηχανισμός του ρολογιού Ρ1 μετρά τον ιδιόχρονο τ1 του ταξιδιού από αριστερά προς δεξιά. Μόλις το Ρ1 φτάσει στο δεξί άκρο, εκτοξεύεται από το δεξί άκρο προς τα αριστερά ένα δεύτερο ρολόι Ρ2, με κάποια άλλη άγνωστη ταχύτητα. Το Ρ2 ταξιδεύει από δεξιά προς αριστερά και μετρά γι αυτό το ταξίδι μια ιδιοχρονική διάρκεια τ2. Ένα τρίτο ρολόι Ρ3 παραμένει ακίνητο στο αριστερό άκρο της ράβδου σε όλη αυτή τη διαδικασία. Το Ρ3 μετρά την διάρκεια τ3 ανάμεσα στο γεγονός «αναχώρηση του Ρ1» και το γεγονός «άφιξη του Ρ2 πίσω στο αριστερό άκρο». Στο τέλος του «πειράματος με τα τρία ρολόγια» γνωρίζουμε μόνο τρεις ιδιοχρόνους: τ1, τ2 και τ3. Δεν έχουμε μετρήσει ούτε ταχύτητες ούτε έχουμε χρησιμοποιήσει χάρακα. Οι Matsas et al χρησιμοποιώντας μόνον τις εν λόγω ενδείξεις τριών ρολογιών υπολογίζουν σχετικά εύκολα(*) το μήκος της ράβδου ως: .
Το σημαντικό είναι ότι δεν χρειάζεται να ξέρουμε τις ταχύτητες των ρολογιών, αλλά ούτε καν την ταχύτητα του φωτός. Χρειαζόμαστε μόνο τρία ρολόγια! Χρησιμοποιούμε τον χρόνο για να μετρήσουμε αποστάσεις με την μονάδα χρόνου μας. Κι αυτό θα εξαγρίωνε τον Woody Allen της ταινίας «Anything Εlse», γιατί δεν είναι δυνατόν να ρωτάει κάποιον «πόσο μήκος έχει η ράβδος» κι αυτός να του απαντάει πέντε δισεκατομμύρια φορές το αντίστροφο της συχνότητας μιας συγκεκριμένης μετάβασης του ατόμου του καισίου.
Και όσον αφορά την μέτρηση της μάζας οι Matsas et al αναφέρονται στο γινόμενο GM – σταθερά της παγκόσμιας έλξης επί μάζα -, που είναι υπεύθυνο για την βαρυτική έλξη και έχει διαστάσεις L3T-2 και κατά συνέπεια, μετριέται με ρολόγια και χάρακες. Τονίζουν ότι αυτή η κοινότοπη γνώση έχει σε μεγάλο βαθμό ξεχαστεί τα τελευταία 150 χρόνια παραθέτοντας το παρακάτω απόσπασμα του Maxwell (A Treatise on Electricity and Magnetism, 1878):
«… η μονάδα μάζας συνάγεται από τις μονάδες χρόνου και μήκους, σε συνδυασμό με το γεγονός της παγκόσμιας βαρύτητας. Η αστρονομική μονάδα μάζας είναι η μάζα που έλκει ένα άλλο σώμα τοποθετημένο σε μια μονάδα απόστασης έτσι ώστε να του προκαλεί μια μονάδα επιτάχυνσης… Αν, όπως στο αστρονομικό σύστημα, η μονάδα μάζας ορίζεται σε σχέση με τη δύναμη έλξης της, τότε οι διαστάσεις της M είναι L3T−2.»
Επομένως η μάζα μπορεί να μετρηθεί με ρολόγια και χάρακες. Και στον σχετικιστικό χωροχρόνο, όπου μπορούμε να μετρήσουμε και το μήκος σε μονάδες χρόνου, μπορούμε να κάνουμε το ίδιο και για την μάζα.
Έχει ενδιαφέρον το γεγονός ότι σε ένα κλασικό Νευτώνειο σύμπαν χρειαζόμαστε και χρονόμετρα και χάρακες, αλλά σε ένα σχετικιστικό σύμπαν, αυτό που περιγράφει η σύγχρονη φυσική, αρκούν μόνο τα χρονόμετρα. Με αυτά μπορούμε να ορίσουμε τις αποστάσεις και εντέλει όλες τις φυσικές ποσότητες.
Με λίγα λόγια, το «όλα είναι ατμός» στην φιλοσοφία του Θανάση Βέγγου ως Θρασύβουλας σε ταινία του 1962:
… πρέπει να αντικατασταθεί με το «όλα είναι χρόνος» .
πηγές:
1. The number of fundamental constants from a spacetime-based perspective – https://www.nature.com/articles/s41598-024-71907-0
2. All of Nature Needs only One Constant, Physicists Prove – https://backreaction.blogspot.com/2025/11/all-of-nature-needs-only-one-constant.html
(*) Εκτός από την εξίσωση που υπολογίζει το μήκος της ράβδου, αξίζει κανείς να δει και την κομψή γεωμετρική αναλογία στο Παράρτημα B της δημοσίευσης των Matsas et al. Εκεί το μήκος της ράβδου συναρτήσει των ιδιοχρόνων συνδέεται με τον τύπο του Ήρωνα που δίνει το εμβαδόν τριγώνου στο διάγραμμα Minkowski.
(Και ένα «άσχετο» σχόλιο. Λίγοι ασχολούνται σήμερα με την Ευκλείδεια Γεωμετρία, αφού το μάθημα στην ουσία έχει εξοριστεί από την μέση εκπαίδευση των δράσεων με αποτέλεσμα οι μαθητές να την περιφρονούν. Περιέργως όμως, κάποιοι φυσικοί, με την δικαιολογία της διαβάθμισης των θεμάτων, επιμένουν να την χρησιμοποιούν ως «μοχλοβραχίονα» για να δημιουργήσουν απεχθή θέματα φυσικής στις πανελλαδικές εξετάσεις: βλέπε ερώτημα Δ1 στα φετινά θέματα.)
Κατηγορίες:ΕΚΠΑΙΔΕΥΣΗ, ΣΧΕΤΙΚΟΤΗΤΑ, ΦΥΣΙΚΗ, ΧΙΟΥΜΟΡ
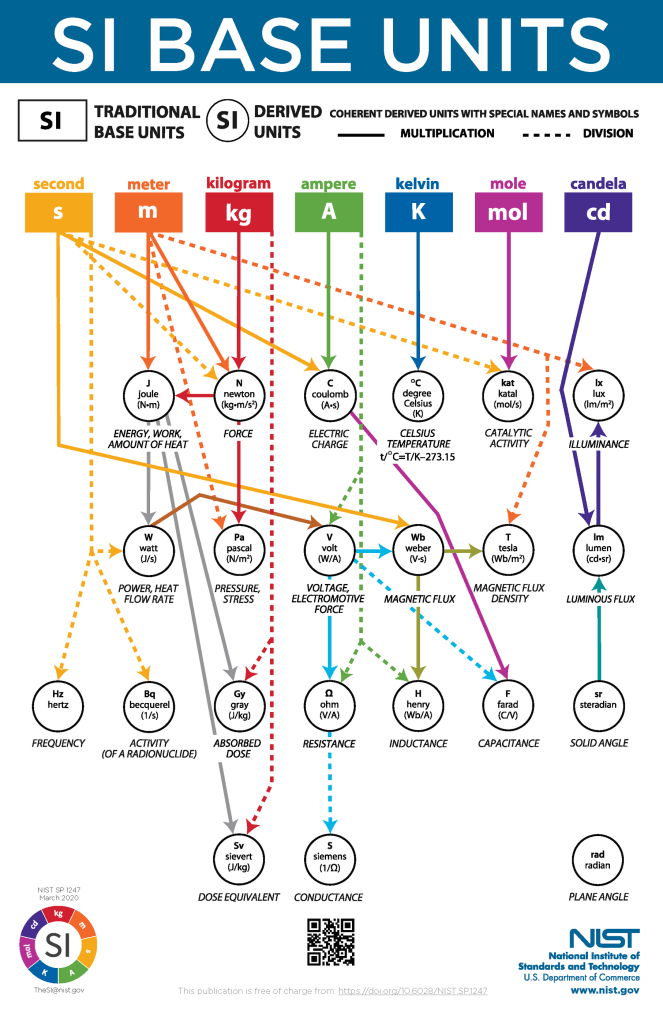
Στο Διεθνές Σύστημα Μονάδων υπάρχουν επτά θεμελιώδεις μονάδες: το δευτερόλεπτο, το μέτρο, το χιλιόγραμμο, το αμπέρ, το κέλβιν, το mole και η καντέλα. Σχεδόν όλοι συμφωνούν ότι οι τέσσερις τελευταίες, αυστηρά μιλώντας, δεν είναι απαραίτητες· μπορούν να υπολογιστούν από τις τρεις πρώτες και τις χρησιμοποιούμε απλώς για ιστορικούς λόγους.
Ένας από αυτούς τους ελάχιστους που διαφωνεί και μία άποψή του για το θέμα:
ΔΙΕΘΝΕΣ ΣΥΣΤΗΜΑ ΜΟΝΑΔΩΝ