Αρχική › ΜΗΧΑΝΙΚΗ › To λάθος του Έντγκαρ Άλαν Πόε …

To λάθος του Έντγκαρ Άλαν Πόε …

By on • ( 6 )

… ή όταν το μήκος ενός εκκρεμούς αυξάνεται κατά την διάρκεια των ταλαντώσεών του

Όσα περιγράφονται παρακάτω θα μπορούσαν να είναι η συνέχεια της παλαιότερης ανάρτησης «Το εκκρεμές του τρόμου«,  που αναφέρεται στο διήγημα του Αμερικανού συγγραφέα Edgar Allan Poe με τίτλο «Το πηγάδι και το εκκρεμές».

Στην ιστορία αυτή ο πρωταγωνιστής ενώ βρίσκεται δεμένος σε ένα κρεβάτι, από πάνω του ταλαντώνεται ένα μεγάλο εκκρεμές. Στο κάτω άκρο του εκκρεμούς υπάρχει μια αιχμηρή μεταλλική λεπίδα, που σιγά – σιγά κατεβαίνει πλησιάζοντας το ανήμπορο θύμα.
Η φονική λεπίδα πλησιάζει όλο και περισσότερο τον πρωταγωνιστή και καθώς το μήκος του εκκρεμούς αυξάνεται, το πλάτος και η ταχύτητα των ταλαντώσεων συνεχώς αυξάνονται.

Pit and the Pendulum 15

Άραγε, όταν το μήκος ενός απλού εκκρεμούς αυξάνεται, τότε αυξάνεται και το πλάτος των ταλαντώσεών του, όπως συμβαίνει με το εκκρεμές του Poe;

pendulum3

Σ’ αυτό το ερώτημα θα απαντήσουμε στη συνέχεια αναλυτικά.

Καταρχήν ας βρούμε την διαφορική εξίσωση που διέπει την κίνηση ενός απλού εκκρεμούς, με σταθερό μήκος, χρησιμοποιώντας (έτσι για … να σπάσουμε τη μονοτονία) την Λαγκρανζιανή του συστήματος (Kινητική ενέργεια μείον Δυναμική ενέργεια):

L = T-V = \frac{1}{2} m v^2 - m g \ell (1 - \cos \theta) = \frac{1}{2} m \ell^{2} \dot{\theta}^2 - m g \ell (1 - \cos \theta)

Από την εξίσωση Lagrange

\frac{d}{dt} ( \partial L / \partial \dot{\theta} ) - \partial L / \partial \theta = 0

προκύπτει η διαφορική εξίσωση

\ddot{\theta}(t) + \frac{g}{\ell} \sin \theta(t) = 0

Η εξίσωση αυτή, παρότι περιγράφει την κίνηση ενός απλού εκκρεμούς (χωρίς τριβές) δεν είναι και τόσο εύκολο να λυθεί. Μόνο στην περίπτωση που θεωρήσουμε ταλαντώσεις με πολύ μικρές γωνίες \sin \theta \sim \theta τότε προκύπτει η διαφορική εξίσωση του απλού αρμονικού ταλαντωτή:

\ddot{\theta}(t) + \frac{g}{\ell} \theta(t) = 0 με τον γνωστό τύπο περιόδου T = \frac{2 \pi}{\omega} = 2 \pi \sqrt{\frac{\ell}{g}}

Στην περίπτωση που προβληματίζεστε για το ποια είναι η μορφή της ακριβούς λύσης του απλού εκκρεμούς δείτε ΕΔΩ:

ακριβής λύση απλού εκκρεμούςDownload

Mελετώντας κανείς το πρόβλημα του εκκρεμούς του Έντγκαρ Άλαν Πόε θα μπορούσε να σκεφτεί ως εξής:
Η διαφορική εξίσωση της κίνησης του εκκρεμούς είναι \ddot{\theta}(t) + \frac{g}{\ell} \sin \theta(t) = 0
Εφόσον το μήκος του εκκρεμούς \ell = \ell(t)  αυξάνεται αργά συναρτήσει του χρόνου, η εξίσωση που περιγράφει την κίνηση γίνεται ακόμη πιο δύσκολη

\ddot{\theta}(t) + \frac{g}{\ell(t)} \sin \theta(t) = 0

Για να πάρουμε μια ιδέα του πως εξελίσσεται η ταλάντωση καθώς αυξάνεται το μήκος, θεωρούμε ένα εύλογο αριθμητικό παράδειγμα θέτοντας: \ell(t)=0,1 t + 10 (και g=10 )
Έτσι προκύπτει
\ddot{\theta}(t) + \frac{10}{0,1 t + 10} \sin \theta(t) = 0
Η τελευταία εξίσωση επιλύεται αριθμητικά χρησιμοποιώντας το πρόγραμμα Mathematica, και η λύση της συμφωνεί σίγουρα  με αυτό που περιγράφει η ιστορία του Poe.
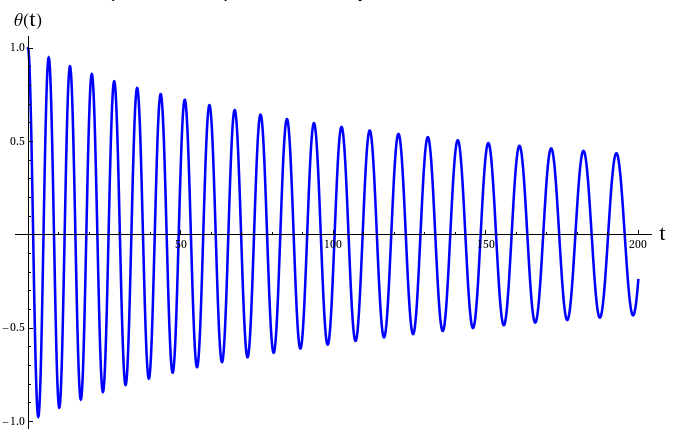
Το γωνιακό πλάτος των ταλαντώσεων αυξάνεται καθώς αυξάνεται το μήκος του εκκρεμούς:

pendulum_poe1
Γραφική παράσταση της αριθμητικής λύσης που δίνει το πρόγραμμα Mathematica

Κι όμως η παραπάνω προσέγγιση είναι εντελώς λανθασμένη! 

Είχε κάνει το ίδιο λάθος και ο Poe; (Ο Poe μάλλον δεν αναφέρεται στο γωνιακό πλάτος των ταλαντώσεων, αλλά στο πλάτος του μήκους τόξου που διαγράφει το εκκρεμές.
Το δεύτερο υπολογίζεται από την εξίσωση s = \theta \ell , και ενώ το μήκος του εκκρεμούς αυξάνεται, η γωνία των ταλαντώσεων, όπως θα δείξουμε στη συνέχεια, μειώνεται).

Το λάθος οφείλεται στην λάθος κατάστρωση της διαφορικής εξίσωση της κίνησης.

Όταν μεταβάλλεται και το μήκος του εκκρεμούς, τότε, δεδομένου ότι τώρα θα υπάρχει και μια ακτινική συνιστώσα της ταχύτητας
v(t) = \sqrt{v^{2}_r + v_{\theta}^2} = \sqrt{\dot{\ell}^{2}(t) + \dot{\theta}^{2}(t) \ell^{2}(t)} , η Λαγκαρανζιανή του συστήματος γίνεται:

L = T-V = \frac{1}{2} m \dot{\ell}^2 + \frac{1}{2} m \ell^{2} \dot{\theta}^2 - m g \ell (1 - \cos \theta)

και η εξίσωση Lagrange δίνει

\frac{d}{dt} ( \partial L / \partial \dot{\theta} ) - \partial L / \partial \theta = 0 \Rightarrow \ell(t) \ddot{\theta}(t) + 2 \dot{\ell}(t) \dot{\theta}(t) + g \sin \theta(t) = 0

Θεωρώντας όπως και πριν: \ell(t)=0,1 t + 10 και g=10 , παίρνουμε τελικά

(0,1 t + 10) \ddot{\theta} + 0,2 \dot{\theta} + 10 \sin \theta = 0

H λύση \theta = \theta(t) (με χρήση του Mathematica) φαίνεται στο επόμενο διάγραμμα:

pendulum_Poe
Η απομάκρυνση θ=θ(t) συναρτήσει του χρόνου

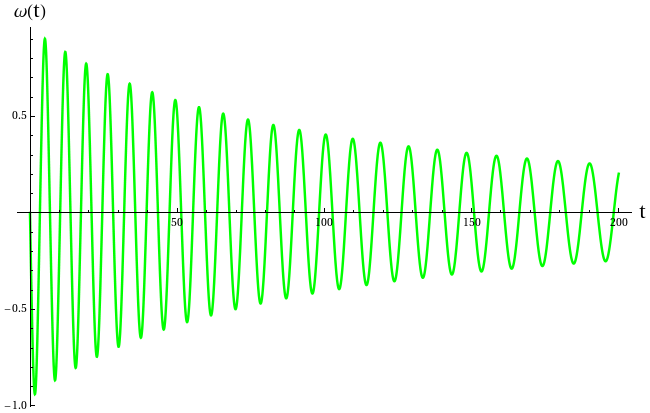
Στο επόμενο διάγραμμα βλέπουμε την γωνιακή ταχύτητα συναρτήσει του χρόνου, \omega = \dot{\theta} = \dot{\theta}(t)

pendulum_omega_Poe
Η γωνιακή ταχύτητα συναρτήσει του χρόνου

Tα αποτελέσματα αυτά δείχνουν ότι καθώς το μήκος του εκκρεμούς αυξάνεται, το γωνιακό πλάτος των ταλαντώσεων μικραίνει, όπως επίσης και το πλάτος της γωνιακής ταχύτητας. Επιπλέον η περίοδος των ταλαντώσεων αυξάνεται.

Τα παραπάνω εξετάζονται επίσης και στην εργασία με τίτλο «Radial Forcing and Edgar Allan Poe’s Lengthening Pendulum» των Matthew McMillan, David Blasing και Heather M. Whitney. Στην εργασία αυτή υπολογίζεται η λύση \theta = \theta(t) , που βλέπουμε στο επόμενο σχήμα , χρησιμοποιώντας το MATLAB (ταυτόσημο με το παραπάνω διάγραμμα του mathematica)

pendulum2


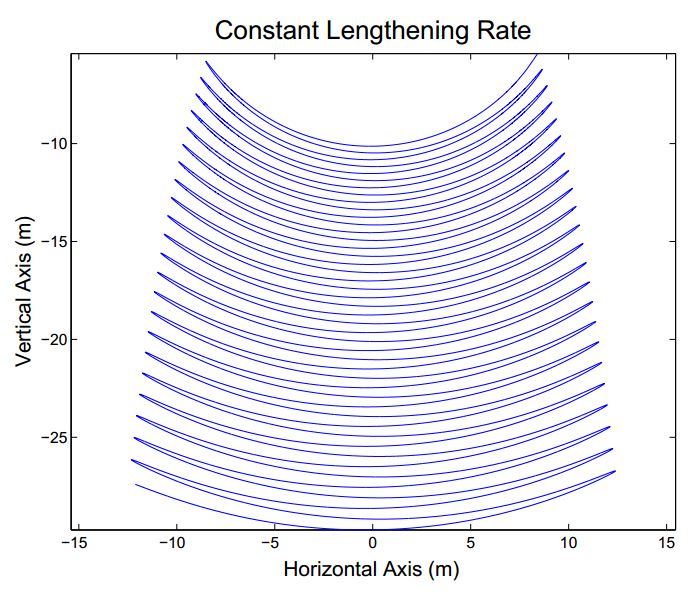
Το επόμενο σχήμα δείχνει την τροχιά του εκκρεμούς (καθώς αυξάνεται το μήκος του)

pendulum_poe

H τροχιά δεν συμφωνεί με τον δραματικό τρόπο που περιγράφεται το φαινόμενο στην ιστορία του Έντγκαρ Άλαν Πόε και στη συνέχεια της εργασίας τους οι συγγραφείς προσπαθούν να εξηγήσουν την κίνηση του εκκρεμούς με κάποιου είδους εξαναγκασμένης ταλάντωση…

Μπορεί οι παραπάνω προβληματισμοί για το εκκρεμές του Poe να προσφέρονται κυρίως για «φιλολογικού» τύπου συζητήσεις σαλονιών,
αποτελούν όμως και μια πρώτης τάξης ευκαιρία για εξάσκηση στην απλή φυσική. Και αυτός ήταν ο σκοπός της παρούσας ανάρτησης.

‹
›

Κατηγορίες:ΜΗΧΑΝΙΚΗ, ΤΑΛΑΝΤΩΣΕΙΣ

Ετικέτες: , ,

6 replies

  1. ggeorge1978
    20/09/2013 • 4:35 μμ

    Υπέροχη ανάλυση!!!

    Τι θα γινόταν όμως εάν δεν αυξανόταν το μήκος του εκκρεμούς αλλά παρέμενε σταθερό και να κατέβαινε το σημείο στήριξης κάθετα προς την γη (δηλαδή όλο το σύστημα μαζί), την χρονική στιγμή που η μάζα του εκκρεμούς έχει περάσει από το σημείο ισορροπίας και κινείται προς τα πάνω;

    Ένας αδρανιακός παρατηρητής (στην περίπτωσή μας το θύμα) θα έβλεπε την αιχμηρή λεπίδα να τον πλησιάζει, το πλάτος ταλάντωσης ή το μήκος τόξου να αυξάνεται, καθώς και την Umax της λεπίδας στην Θ.Ι. να αυξάνεται.

    Δεν έχω διαβάσει το βιβλίο και δεν ξέρω εάν ο συγγραφέας αναφέρει ξεκάθαρα ότι το μήκος του εκκρεμούς αυξάνεται, γιατί αλλιώς υπάρχει και η παραπάνω περίπτωση.

    Reply ↓
    • physicsgg
      20/09/2013 • 6:34 μμ

      Καλό ερώτημα! Νομίζω ότι στην περίπτωση αυτή η κίνηση του εκκρεμούς δεν αλλάζει, ο πρωταγωνιστής όμως θα «βλέπει» και μια κατακόρυφη συνιστώσα στην ταχύτητα.
      ‘Ετσι, λόγω της αρχής ανεξαρτησίας κινήσεων, καθώς όλο το σύστημα θα κατεβαίνει,
      το μέτρο της ταχύτητα του εκκρεμούς θα φαίνεται μεγαλύτερο στον κρατούμενο … και κυρίως πιο «τρομακτικό».

      Reply ↓
      • ggeorge1978
        20/09/2013 • 7:08 μμ

        Αυτό ακριβώς θα συνέβαινε αν το σύστημα του εκκρεμούς κινούνταν κάθετα με σταθερή ταχύτητα.
        Αυτό που λέω εγώ είναι ότι αρχικά το σύστημα είναι σταθερό. Σε κάποια χρονική στιγμή, όταν η μάζα του εκκρεμούς έχει περάσει από την Θ.Ι. και έχει ανοδική πορεία και λίγο πριν φτάσει στο ανώτατο σημείο, το σύστημα διαγράφει ελεύθερη πτώση έως ότου διανύσει πχ 1cm και μετά ακαριαία σταματήσει πάλι. Λόγω της κινητικής ενέργειας που θα έχει η μάζα του εκκρεμούς, θα συνεχίσει την ανοδική πορεία αλλά τελικά θα έχει αποκτήσει περισσότερη δυναμική ενέργεια (η Θ.Ι. έχει πάει πιο χαμηλά) και θα έχει μεγαλύτερο μήκος τόξου να διανύσει.
        (Θεωρώ ότι η μάζα του εκκρεμούς είναι συνδεδεμένη με αβαρής ράβδος, και την ροπή δύναμης που θα ασκηθεί στο σύστημα ράβδου/μάζας κατά το χρονικό διάστημα Δt της ελεύθερης πτώσης, αμελητέα)

        Reply ↓
        • physicsgg
          20/09/2013 • 7:37 μμ

          Στην περίπτωση αυτή αλλάζει το πράγμα… Να επισημάνω μόνο ότι αν το σύστημα του εκκρεμούς αφεθεί να εκτελέσει ελεύθερη πτώση, τότε κατά τη διάρκεια της πτώσης το βάρος «εξουδετερώνεται» και δεν υπάρχει ταλάντωση.

          Reply ↓
          • ggeorge1978
            19/09/2014 • 12:24 πμ

            Ακριβώς!!!

            Όπως πχ όταν έχουμε ένα εκκρεμές στερεωμένο στον τοίχο ενός ανελκυστήρα. Το εκκρεμές ταλαντεύεται με μέγιστη γωνία φ από την θέση ισορροπίας και κάποια τυχαία χρονική στιγμή t αφήνουμε τον ανελκυστήρα να εκτελέσει ελεύθερη πτώση. Θα διακρίνουμε 2 περιπτώσεις:

            α) Αν την χρονική στιγμή t το εκκρεμές βρίσκεται στο ανώτατο σημείο του, όπου και η στιγμιαία γωνιακή του ταχύτητα είναι μηδέν, τότε θα αφεθεί να εκτελέσει ελεύθερη πτώση. (Ένας μη αδρανιακός παρατηρητής που βρίσκεται μέσα στον ανελκυστήρα θα το δει να παραμένει ακίνητο)

            β) Αν την χρονική στιγμή t το εκκρεμές βρίσκεται σε οποιοδήποτε άλλο σημείο της κίνησής του, όπου και η στιγμιαία γωνιακή του ταχύτητα ω είναι διάφορη του μηδενός, τότε θα συνεχίσει να περιφέρεται γύρω από σημείο στήριξης με σταθερή γωνιακή ταχύτητα λόγω της στροφορμής του. (Ένας μη αδρανιακός παρατηρητής που βρίσκεται μέσα στον ανελκυστήρα θα το δει να εκτελεί ομαλή κυκλική κίνηση)

            Οπότε, εάν έχουμε ένα εκκρεμές μάζας m στερεωμένο σε μια βάση στήριξης μάζας Μ, όπου Μ>>m (ώστε κατά την ελεύθερη πτώση το κέντρο μάζας του συστήματος του συστήματος να ταυτίζεται σχεδόν με κάθετο άξονα που περνάει από το σημείο στήριξης), τότε θα παρατηρήσουμε συμπεριφορά παρόμοια με την παραπάνω.
            Αν το σύστημα αυτό, λίγο πριν φτάσει το εκκρεμές στην μέγιστη γωνία του, το αφήσουμε να εκτελέσει ελεύθερη πτώση τόσο ώστε χάριν της στροφορμής του η μάζα του εκκρεμούς φτάσει γωνία μεγαλύτερη της μέγιστης και αμέσως το σταματήσουμε απότομα, τότε θα έχουμε κερδίσει ενεργειακά κ.ο.κ.

            Άρα, εάν ο συγγραφέας δεν αναφέρει ξεκάθαρα ότι το μήκος του εκκρεμούς αυξάνεται, τότε άδικα τον κατηγορούμε… 🙂

            Reply ↓
          • ggeorge1978
            20/09/2014 • 3:32 μμ

            Και όχι μόνο. Το Δt της ελεύθερης πτώσης μπορεί να είναι τέτοιο ώστε να υπερνικήσει και τυχόν απόσβεση τριβών σε ένα πιο ρεαλιστικό σενάριο…

            Reply ↓

Σχολιάστε

Ο ιστότοπος χρησιμοποιεί το Akismet για την εξάλειψη των ανεπιθύμητων σχολίων. Μάθετε πως επεξεργάζονται τα δεδομένα των σχολίων σας.