H σειρά Taylor γύρω από το σημείο x=α περιγράφεται από την εξίσωση

Η σειρά Maclaurin είναι η σειρά Taylor γύρω από το σημείο x=0
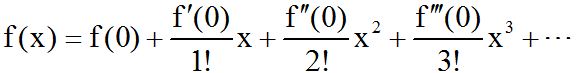Έστω ότι η συνάρτηση που αναπτύσσεται σε σειρά Maclaurin είναι η θέση x(t) μιας μονοδιάστατης επιταχυνόμενης κίνησης. Τότε (δεδομένου ότι τώρα η ελεύθερη μεταβλητή είναι ο χρόνος t) θα έχουμε:

Η παραπάνω εξίσωση είναι η εξίσωση της θέσης στην πιο γενική μορφή επιταχυνόμενης κίνησης (σε μια διάσταση).
Για παράδειγμα στην περίπτωση της ευθύγραμμης ομαλά επιταχυνόμενης κίνησης θα ισχύει:

διότι
• έστω ότι το σώμα τη χρονική στιγμή t=0 βρίσκεται στη θέση x(0)=0
• η πρώτη παράγωγος της θέσης την χρονική στιγμή t=0 είναι η αρχική ταχύτητα:

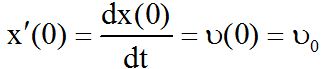
• και η δεύτερη παράγωγος ή η πρώτη παράγωγος της ταχύτητας (ο ρυθμός μεταβολής της ταχύτητας) είναι η επιτάχυνση:

• η παράγωγοι ανώτερης τάξης (εφόσον η δεύτερη παράγωγος είναι σταθερή) θα είναι μηδέν

και έτσι προκύπτει η – παγκοσμίως γνωστή στους μαθητές της Α’Λυκείου – εξίσωση της μετατόπισης (Δx=x-x₀=x, δεδομένου ότι x₀=0) στην ευθύγραμμη ομαλά επιταχυνόμενη κίνηση

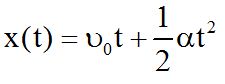
Διαβάστε επίσης (σχετικά με την εφαρμογή της σειράς Taylor στη φυσική): Η ατέρμονη επανάληψη του αρμονικού ταλαντωτή

Κατηγορίες:ΜΗΧΑΝΙΚΗ

Ετικέτες: Επιταχυνόμενη Κίνηση, Maclaurin, Taylor