Είναι δυνατόν μια ιδιότητα ενός σωματιδίου να βρίσκεται σε διαφορετική θέση από το ίδιο το σωματίδιο; Η πόλωση ενός φωτονίου, για παράδειγμα, θα μπορούσε να βρίσκεται σε ένα εντελώς διαφορετικό σημείο από το ίδιο το φωτόνιο; Αν κάτι τέτοιο είναι δυνατόν να πραγματοποιηθεί, τότε μιλάμε για το αμφιλεγόμενο φαινόμενο του κβαντικού γάτου του Τσέσαϊρ.
Το όνομα προέρχεται από τον γάτο του Τσέσαϊρ (Cheshire) στο παραμύθι «Η Αλίκη στη χώρα των θαυμάτων» του Lewis Carroll, ο οποίος εξαφανιζόταν αφήνοντας πίσω μόνο το χαμόγελό του:
«Εντάξει», είπε ο Γάτος· και αυτή τη φορά εξαφανίστηκε αρκετά αργά, ξεκινώντας από την άκρη της ουράς και τελειώνοντας με το χαμόγελο, το οποίο παρέμεινε αρκετή ώρα αφότου είχε εξαφανιστεί το υπόλοιπο σώμα.
«Λοιπόν! Έχω δει συχνά μια γάτα χωρίς χαμόγελο», σκέφτηκε η Αλίκη, «αλλά ένα χαμόγελο χωρίς γάτα! Είναι το πιο περίεργο πράγμα που έχω δει ποτέ στη ζωή μου!»
Δεν είναι περίεργο που η Αλίκη εκπλήσσεται. Στην πραγματική ζωή, υποθέτοντας ότι οι γάτες όντως χαμογελούν, το χαμόγελο είναι ιδιότητα της γάτας – δεν έχει νόημα να σκεφτόμαστε ένα χαμόγελο χωρίς γάτα. Και αυτό ισχύει για σχεδόν όλες τις φυσικές ιδιότητες. Για παράδειγμα, η πόλωση είναι ιδιότητα των φωτονίων. Δεν έχει νόημα να μιλάμε για πόλωση χωρίς φωτόνιο. Ωστόσο, όπως υποστήριξαν για πρώτη φορά οι Yakir Aharonov et al στη δημοσίευσή τους το 2013 με τίτλο Quantum Cheshire Cats (New J. Phys. 15 113015), η πόλωση των φωτονίων μπορεί να υπάρχει εκεί που δεν υπάρχει καθόλου φωτόνιο.
Πλέον ακούγεται βαρετό να λέμε ότι τα πράγματα είναι παράξενα στον κβαντικό κόσμο. Αλλά μπορούν να γίνουν πολύ πιο παράξενα, όταν η ιδιότητα ενός σωματιδίου φαίνεται να βρίσκεται σε διαφορετική θέση από το ίδιο το σωματίδιο, όπως η πόλωση ενός φωτονίου μπορεί να υπάρχει σε εντελώς διαφορετικό σημείο από το ίδιο το φωτόνιο· κι αυτό είναι μια κβαντική γάτα του Τσέσαϊρ.
Αν και η προοπτική «ασώματων ιδιοτήτων» μπορεί να φαίνεται ανησυχητική, αποτελεί έναν τρόπο ερμηνείας των κομψών προβλέψεων της κβαντικής μηχανικής. Αυτή τουλάχιστον ήταν η σκέψη όταν οι Yakir Aharonov, Sandu Popescu, Daniel Rohrlich και Paul Skrzypczyk παρουσίασαν για πρώτη φορά τις κβαντικές γάτες του Τσέσαϊρ.
Για να κατανοήσει κανείς την έννοια, πρέπει να θυμηθεί ότι μια μέτρηση σε κβαντικό σύστημα το «καταρρέει» σε μία από τις ιδιοκαταστάσεις του – όπως όταν ανοίγεις το κουτί και βρίσκεις τη γάτα του Σρέντινγκερ είτε νεκρή είτε ζωντανή. Ωστόσο, παίζοντας μεταξύ του βαθμού παρεμβατικότητας της μέτρησης και της αβεβαιότητας του αποτελέσματος, μπορεί κανείς να αποσπάσει ελάχιστη πληροφορία διαταράσσοντας ελάχιστα το σύστημα. Αν μια τέτοια μέτρηση επαναληφθεί πολλές φορές ή σε σύνολο σωματιδίων, τα αποτελέσματα μπορούν να ληφθούν κατά μέσο όρο και να δώσουν ακριβή τιμή. Η μέθοδος απόσπασης πληροφορίας από ένα κβαντικό σύστημα μέσω μέσω μετρήσεων που αλληλεπιδρούν πολύ ασθενώς με το σύστημα, έτσι ώστε κάθε μεμονωμένη μέτρηση να μη λέει τίποτε αλλά ο μέσος όρος πολλών επαναλήψεων να δίνει χρήσιμη πληροφορία, είναι γνωστή ως «ασθενής μέτρηση» και προτάθηκε για πρώτη φορά το 1980.
Αν και η ιδέα της ασθενούς μέτρησης δεν φαίνεται καθεαυτή να αποτελεί ριζική απομάκρυνση από τον κβαντικό φορμαλισμό, μας αποκαλύπτει «έναν εντελώς νέο κόσμο». Ο Aharonov και οι συνεργάτες του έχουν περάσει τις τελευταίες τέσσερις δεκαετίες εξετάζοντας κάθε είδους σενάρια στα οποία η ασθενής μέτρηση μπορεί να οδηγήσει σε απρόσμενες συνέπειες, και η κβαντική γάτα του Τσέσαϊρ ήταν ένα από τα φαινόμενα που ανακάλυψαν τυχαία.
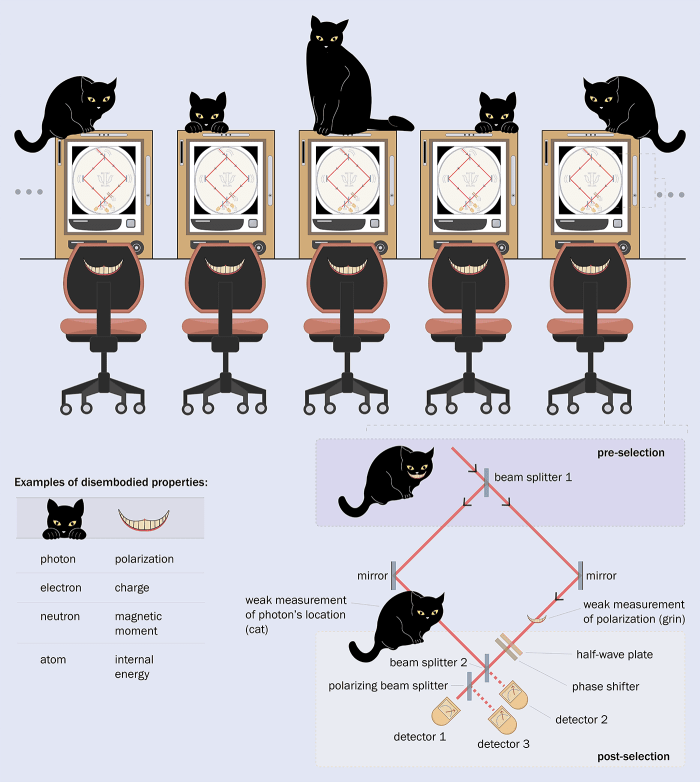
Στην εργασία τους του 2013, ο Aharonov και οι συνεργάτες του φαντάστηκαν μια απλή διάταξη οπτικού συμβολόμετρου, όπου η «γάτα» είναι ένα φωτόνιο που μπορεί να βρίσκεται είτε στον αριστερό είτε στον δεξιό βραχίονα, ενώ το «χαμόγελο» είναι η κυκλική πόλωση του φωτονίου. Η γάτα (το φωτόνιο) προετοιμάζεται αρχικά σε μια κατάσταση υπέρθεσης, γνωστή ως προ-επιλογή. Αφού εισέλθει στη διάταξη, η γάτα μπορεί να εξέλθει από διάφορες πιθανές εξόδους. Ο αποχωρισμός μεταξύ σωματιδίου και ιδιότητας εμφανίζεται στις περιπτώσεις όπου το σωματίδιο εξέρχεται από μια συγκεκριμένη έξοδο (post-selection).
Κατά τη διάρκεια που το σωματίδιο βρίσκεται μέσα στο συμβολόμετρο (μεταξύ προ- και μετα-επιλογής), πραγματοποιούνται ορισμένες μετρήσεις που αναλύουν τις ιδιότητές του. Επειδή πρόκειται για ασθενείς μετρήσεις, πρέπει να εκτελεστούν πολλές φορές ώστε να προσδιοριστεί ο μέσος όρος. Για συγκεκριμένους συνδυασμούς προ- και μετα-επιλογής, διαπιστώνεται ότι η γάτα βρίσκεται στον αριστερό βραχίονα, ενώ το χαμόγελο στον δεξιό. Είναι μια γάτα του Τσέσαϊρ αποχωρισμένη από το χαμόγελό της.
Η μαθηματική περιγραφή αυτής της παράξενης κατάστασης ήταν σαφής, αλλά η ερμηνεία της φαινόταν παράλογη και το αρχικό άρθρο χρειάστηκε πάνω από έναν χρόνο αξιολόγησης πριν δημοσιευθεί, προκαλώντας παρ’ όλα αυτά επικρίσεις. Λίγο αργότερα, πειράματα με πολωμένα νετρόνια (Nature Comms 5 4492) και φωτόνια (Phys. Rev. A 94 012102) δοκίμασαν την αρχική διάταξη της ομάδας. Ωστόσο, αυτά τα πειράματα και οι επακόλουθες δοκιμές, παρότι επιβεβαίωσαν τις θεωρητικές προβλέψεις, δεν έλυσαν την διαμάχη· το πρόβλημα άλλωστε βρισκόταν στην ερμηνεία.
Ένα κβάντο πιθανοτήτων
Για να συμφιλιωθεί κανείς με αυτή την αινιγματική ιδέα, μπορεί να φανταστεί την προ- και μετα-επιλεγμένη διάταξη σαν ένα μηχάνημα pachinko, όπου μια μπίλια ξεκινά από επάνω σε μία προεπιλεγμένη θέση και κατεβαίνει μέσα από διάφορα εμπόδια για να καταλήξει σε ένα συγκεκριμένο σημείο (τη μετα-επιλογή): την τρύπα του τζάκποτ. Αν μετρήσουμε πόσες μπίλιες πέφτουν στην τρύπα του τζάκποτ, μπορούμε να υπολογίσουμε την κατανομή πιθανοτήτων. Στον κλασικό κόσμο, είναι δυνατόν να μετρηθεί η θέση και οι ιδιότητες της μπίλιας σε διαφορετικά σημεία, π.χ. με μια κάμερα.
Η παρατήρηση αυτή δεν θα επηρεάσει την τροχιά της μπίλιας ούτε την πιθανότητα να πετύχει το τζάκποτ. Σε μια κβαντική εκδοχή του μηχανήματος pachinko, η προ- και μετα-επιλογή λειτουργούν με παρόμοιο τρόπο, με τη διαφορά ότι μπορεί να τροφοδοτηθεί με μπίλιες σε καταστάσεις υπέρθεσης. Μια ασθενής μέτρηση δεν διαταράσσει το σύστημα, οπότε πολλαπλές μετρήσεις μπορούν να αποκαλύψουν τις πιθανότητες ορισμένων αποτελεσμάτων. Το αποτέλεσμα της μέτρησης δεν δίνει μια ιδιοτιμή – που αντιστοιχεί σε φυσική ιδιότητα του συστήματος- αλλά «ασθενείς τιμές», των οποίων η ερμηνεία δεν είναι ξεκάθαρη.
Για να το κατανοήσουμε αυτό σε κβαντικό πλαίσιο, χρειαζόμαστε μια διαισθητική νοητική εικόνα, έστω περιορισμένη. Γι’ αυτό οι κβαντικές γάτες του Τσέσαϊρ αποτελούν μια ισχυρή μεταφορά, αλλά και κάτι περισσότερο, καθώς καθοδηγούν τους ερευνητές σε νέες κατευθύνσεις. Πράγματι, από την αρχική ανακάλυψη, οι Aharonov, Popescu και οι συνεργάτες τους έχουν συναντήσει κι άλλες εκπλήξεις.
Το 2021 οι ερευνητές γενίκευσαν το φαινόμενο της κβαντικής γάτας του Τσέσαϊρ σε μια δυναμική εκδοχή, όπου η «ασώματη» ιδιότητα μπορεί να διαδίδεται στο χώρο (A dynamical quantum Cheshire Cat effect and implications for counterfactual communication). Για παράδειγμα, μπορεί να υπάρξει στροφορμή χωρίς κάτι που να τη μεταφέρει (Angular momentum flow without anything carrying it). Σε άλλη γενίκευση, ο Aharonov φαντάστηκε ένα σωματίδιο με μάζα που θα μπορούσε να μετρηθεί σε ένα σημείο χωρίς ορμή, ενώ η ορμή του θα μπορούσε να μετρηθεί αλλού χωρίς τη μάζα του!
Προκλητικές ερμηνείες
Αν βρίσκεις αυτές τις ιδέες αλλοπρόσαλλες, δεν είσαι μόνος. «Είναι σπαζοκεφαλιές», εξηγεί ο φυσικός Jonte Hance, Στην πραγματικότητα, ο Hance πιστεύει ότι οι κβαντικές γάτες του Τσέσαϊρ είναι εξαιρετικός τρόπος για να προκληθεί ενδιαφέρον για τα θεμέλια της κβαντικής μηχανικής. Οι φυσικοί ήταν υπερβολικά απασχολημένοι εφαρμόζοντας την κβαντική μηχανική σε διάφορα προβλήματα, για να ασχοληθούν με θεμελιώδη ερωτήματα.
Βέβαια, τα πρώτα χρόνια της κβαντικής φυσικής σημαδεύτηκαν από διάσημες διαμάχες ανάμεσα στον Niels Bohr και τον Albert Einstein, οι οποίες κορυφώθηκαν με την κριτική στο παράδοξο Einstein–Podolski–Rosen (EPR) (Phys. Rev. 47 777) το 1935. Όμως στη συνέχεια οι φυσικοί ήταν πολύ απασχολημένοι με πρακτικές εφαρμογές της θεωρίας για να ενδιαφερθούν για τα θεμέλια της.
Αυτή η έλλειψη ενδιαφέροντος για τα θεμέλια της κβαντικής μηχανικής φαίνεται καθαρά μέσα από δύο ιστορίες, η πρώτη από τις οποίες αφορά τον ίδιο τον Aharonov. Όταν ο Aharonov σπούδαζε φυσική στο Technion του Ισραήλ τη δεκαετία του 1950, ρώτησε τον Nathan Rosen (το R του EPR) αν θα μπορούσε να εργαστεί πάνω στα θεμέλια της κβαντικής μηχανικής. Το θέμα δεν ήταν καθόλου της μόδας, ώστε ο Rosen τον συμβούλεψε να επικεντρωθεί στις εφαρμογές. Ευτυχώς, ο Aharonov αγνόησε τη συμβουλή και συνέχισε να εργάζεται με τον Αμερικανό κβαντικό θεωρητικό David Bohm.
Όταν άρχισαν να αναπτύσσονται η κβαντική πληροφορική και οι κβαντικοί υπολογιστές, σημειώθηκε μια σύντομη αναγέννηση του ενδιαφέροντος για τα θεμέλια της θεωρίας, η οποία κορυφώθηκε στις αρχές της δεκαετίας του 2010. Όμως την τελευταία δεκαετία το ερευνητικό ενδιαφέρον έχει επανέλθει σταθερά στις εφαρμογές.
Παρά τις συνεχείς υπενθυμίσεις της εκλαϊκευμένης επιστήμης για το πόσο «παράξενη» είναι η κβαντική μηχανική, οι φυσικοί συχνά υιοθετούν την πραγματιστική στάση του «σκάσε και υπολόγισε». Ο Hance αναφέρει ότι οι ερευνητές «συνήθως ξεχνούν πόσο παράξενη είναι η κβαντική μηχανική· κι όμως αυτή η δαίσθηση του παράξενου είναι απαραίτητη». Πράγματι, παράδοξα όπως της γάτας του Σρέντινγκερ και του EPR έχουν ελκύσει και εμπνεύσει γενιές φυσικών και υπήρξαν καθοριστικά στην ανάπτυξη των κβαντικών τεχνολογιών.
Ο σκοπός της κβαντικής γάτας του Τσέσαϊρ και παρόμοιων παραδόξων είναι να προκαλέσουν τη διαισθησή μας και να μας ωθήσουν να σκεφτούμε έξω από τα συνηθισμένα όρια. Αυτό είναι σημαντικό ακόμα κι αν οι πρακτικές εφαρμογές δεν είναι άμεσα ορατές. Σύμφωνα με τον Popescu: «Οι περισσότεροι συμφωνούν ότι αν και γνωρίζουμε τους βασικούς νόμους της κβαντικής μηχανικής, δεν καταλαβαίνουμε πραγματικά τι είναι η κβαντική μηχανική».
Το ερευνητικό πρόγραμμα του Aharonov και των συνεργατών του επιδιώκει να αναπτύξει μια σωστή διαισθητική αντίληψη που θα μας οδηγήσει παραπέρα. «Πιστεύουμε βαθιά ότι μπορεί να βρεθεί ένας διαισθητικός τρόπος σκέψης για την κβαντική μηχανική», προσθέτει ο Popescu. Κι αυτός μπορεί να περιλαμβάνει ή να μην περιλαμβάνει γάτους.
Κλείνοντας ας τονίσουμε ότι το φαινόμενο του «κβαντικού γάτου του Τσέσαϊρ» δεν σημαίνει πως μια ιδιότητα διαχωρίζεται από το σωματίδιο και «ταξιδεύει» μόνη της. Κατ’ αρχήν ο διαχωρισμός προκύπτει μόνο κάτω από πολύ συγκεκριμένες συνθήκες (προ-επιλογή, ασθενείς μετρήσεις, μετα-επιλογή). Και αφορά τις λεγόμενες ασθενείς τιμές (weak values) – τις ειδικές μέσες τιμές που προκύπτουν μόνο με αυτό το είδος μετρήσεων και δεν ταυτίζονται με τις συνηθισμένες ιδιοτιμές ενός παρατηρήσιμου μεγέθους (observable). Το εξωτικό φαινόμενο είναι ένα χαρακτηριστικό της μεθόδου μέτρησης, όχι μια αληθινή διάσπαση αντικειμένου και ιδιότητας. Δεν καταφέρνουμε τον διαχωρισμό του γάτου από το χαμόγελό του, αλλά διαπιστώνουμε ότι το κβαντικό σύστημα επιτρέπει οι ενδείξεις μιας ιδιότητας να “διαχωρίζονται στατιστικά” από τις ενδείξεις της θέσης του φορέα της.
Διαβάστε περισσότερες λεπτομέρειες στο άρθρο: Curiouser and curiouser: delving into quantum Cheshire cats- https://physicsworld.com/a/curiouser-and-curiouser-delving-into-quantum-cheshire-cats/
Κατηγορίες:ΚΒΑΝΤΙΚΗ ΘΕΩΡΙΑ

Τι σημαίνει να υπάρχει πόλωση χωρίς φωτόνιο ή σπιν χωρίς σωματίδιο; Η φυσική ασχολείται με ότι μπορεί να μετρηθεί. Τι μετράμε σ’ αυτές τις περιπτώσεις; Κάτι δεν καταλαβαίνω….
Εγώ καταλαβαίνω το εξής:
Σε μια μεγα΄λη ήρεμη λίμνη βρίσκεται ένα ψάρι και θέλουμε να μάθουμε που βρίσκεται και τι χρώμα έχει. Αν ρίξω δίχτυ σε μια περιοχή της λίμνης μπορεί να το πιάσω (ή όχι), κι αν το πιάσω θα έχω προσδιορίσει και τη θέση του και το χρώμα του. Αυτή είναι μια «ισχυρή» μέτρηση.
Όμως οι Aharonov και λοιποί εκτελούν «ασθενείς μετρήσεις».
Η λίμνη τους διαθέτει δύο είδη «ασθενών» ανινιχνευτών:
α) υπάρχουν καλαμιές που είναι στερεωμένες στον πυθμένα που αν το ψάρι περάσει δίπλα τους κινούνται σχεδόν ανεπαίσθητα, με δόνηση τόσο μικρή που δεν τρομάζει το ψάρι και δεν αλλάζει πορεία του. Αλλα από μόνη της δεν μας λέει τίποτε (ασθενής μέτρηση θέσης)
β) στη λίμνη υπάρχουν επίσης και φύκια με την ιδιότητα να αλλάζουν ελάχιστα το χρώμα τους όταν το ψάρι περνάει δίπλα τους. Αυτά τα φύκια δεν επηρεάζουν καθόλου την πορεία του ψαριού, αλλά δίνουν μια ανεπαίσθητη αλλαγή χρώματος. Αλλά από μόνη της δεν μας λέει τίποτε (ασθενής μέτρηση της ιδιότητας-πόλωση)
Από μόνες τους οι παρατηρήσεις των ανεπαίσθητων δονήσεων των καλαμιών και των αντανακλάσεων των φυκιών δεν μας λένε τίποτα για την θέση και το χρώμα του ψαριού. Αν όμως πραγαμτοποιήσουμε πολυάριθμες μετρήσεις, αυτές οι αμφίβολες ενδείξεις μας δείχνουν μια στατιστική εικόνα από διέρχεται το ψάρι (ανιχνευτές-καλάμια) και που εμφανίζεται η ιδιότητά του(ανιχνευτές-φύκια).
Έστω τώρα ότι πραγματοποιούμε τις παρατηρήσεις μας μόνο όταν το ψάρι ξεκινά την πορεία του από μια συγκεκριμένη περιοχή π.χ. νότια πλευρά της λίμνης(preselection) επιλέγοντας έτσι την «αρχική του κατάσταση». Kαι κρατάμε τα αποτελέσματα όταν αυτό καταλήγει σε μια συγκεκριμένη όχθη (postselection). Αν κρατήσουμε τις μετρήσεις στις οποίες το ψάρι κατέληξε π.χ. στην δυτική όχθη, αυτή η μετα-επιλογή αλλάζει ριζικά την στατιστική εικόνα που παίρνουμε από τις ασθενείς μετρήσεις. Όταν κάνουμε κα΄τι τέτοιο, τότε μπορεί να προκύψει το παράδοξο ότι το ψάρι πέρασε π.χ. κυρίως από τη βόρεια πλευρά, ενώ τα χαρακτηριστικά του εμφανίστηκαν στη νότια πλευρά.
Αυτό σημαίνει ότι οι ασθενείς ενδείξεις της θέσης και της ιδιότητας (μετά το post-selection) αποκλίνουν στατιστικά. Κι αυτό είναι το ανάλογο του κβαντικού χαμόγελου χωρίς τον γάτο.
Εγώ καταλαβαίνω ότι τα γατιά είναι τα αγαπημένα ζώα των Φυσικών!