Αρχική › ΜΑΘΗΜΑΤΙΚΑ › Μια οπτική αποδειξη της ανισότητας π^e < e^π

Μια οπτική αποδειξη της ανισότητας π^e < e^π

By on • ( 3 )

Σε ένα από τα πιο σύντομα άρθρα μαθηματικών (ΕΔΩ) αποδεικνύεται με έναν οπτικό τρόπο ότι

\pi^{e}<e^{\pi}

ως εξής:

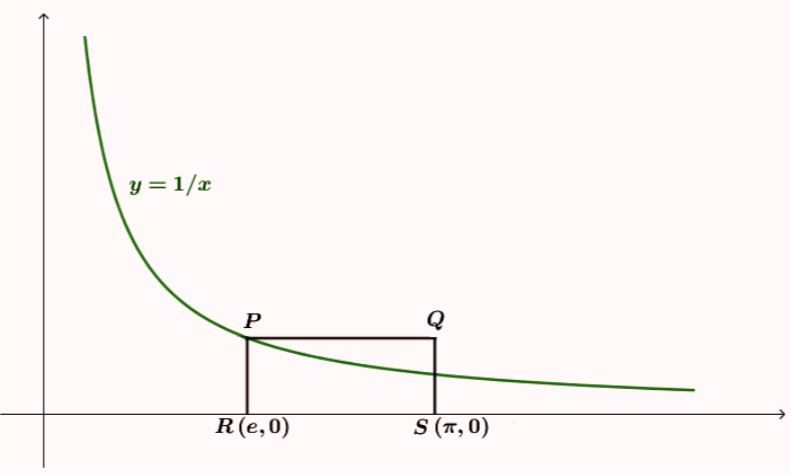
Aπό το παραπάνω σχήμα συγκρίνοντας εμβαδά προκύπτει ότι:

\ln \pi - 1= \int_{e}^{\pi} \frac{1}{x} dx < \frac{1}{e}(\pi -e) \Rightarrow \ln \pi <\frac{\pi}{e} \Rightarrow \pi^{e}<e^{\pi}

Μια άλλη επίσης οπτική απόδειξη είναι η εξής:

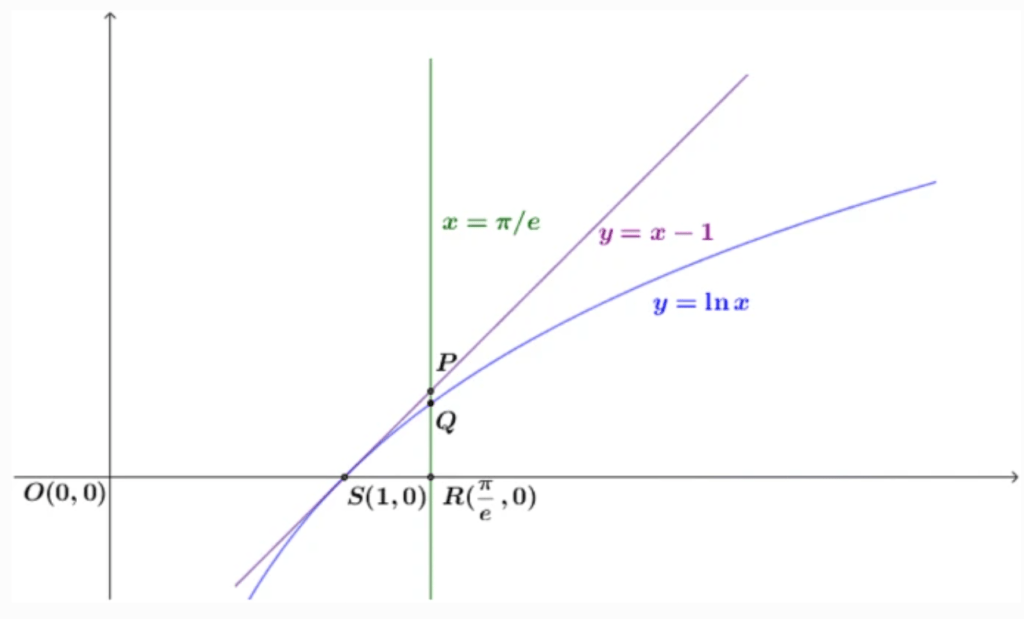
Από το παραπάνω σχήμα προκύπτει ότι:

\ln \frac{\pi}{e} = QR < PR = \frac{\pi}{e}-1 ή

\ln \frac{\pi}{e} < \frac{\pi}{e} -1 \Rightarrow \frac{\pi}{e} < e^{\frac{\pi}{e}-1} \Rightarrow \pi^{e}<e^{\pi}

πηγές: https://link.springer.com/article/10.1007%2Fs00283-018-9816-4 – https://link.springer.com/article/10.1007/s00283-018-09867-3

‹
›

Κατηγορίες:ΜΑΘΗΜΑΤΙΚΑ

Ετικέτες:

3 replies

  1. eigenspace's avatar
    eigenspace
    03/05/2021 • 2:07 μμ

    Χρόνια πολλά σε όλη την ομάδα. Παρακαλώ διορθώστε το p σε π, στον τίτλο του άρθρου, για εμάς τους ψυχαναγκαστικούς.
    χαχαχαχαχα!
    Να είστε καλά!

    Reply ↓

Αφήστε απάντηση στον/στην physicsgg Ακύρωση απάντησης

Ο ιστότοπος χρησιμοποιεί το Akismet για την εξάλειψη των ανεπιθύμητων σχολίων. Μάθετε πως επεξεργάζονται τα δεδομένα των σχολίων σας.