Αρχική › ΜΑΘΗΜΑΤΙΚΑ › Oλίσθηση σε κεκλιμένα επίπεδα και ο νόμος του Snell

Oλίσθηση σε κεκλιμένα επίπεδα και ο νόμος του Snell

By on • ( 2 )

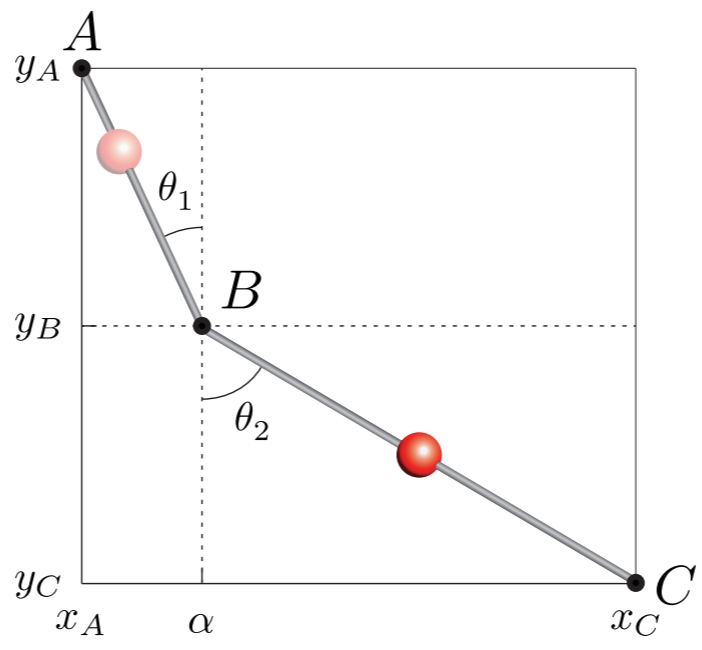
Η σημειακή χάντρα του παραπάνω σχήματος ολισθαίνει χωρίς τριβές κατά μήκος των ευθύγραμμων οδηγών ΑΒ και ΒC.
1. Aν v_{A} , v_{B} και v_{C} είναι οι ταχύτητες που έχει η χάντρα στα σημεία A, Β και C. Να δείξετε ότι η μέση ταχύτητα για την διαδρομή ΑΒ είναι: \bar{v}_{1}=\frac{v_{A}+v_{B}}{2}=\frac{v_{A} +\sqrt{2g(y_{A}-y_{B})}}{2} και για την διαδρομή ΒC: \bar{v}_{2}=\frac{v_{B}+v_{C}}{2}=\frac{\sqrt{2g(y_{A}-y_{B})}+\sqrt{2g(y_{A}-y_{C})}}{2}
2. Θεωρούμε τα σημεία Α και C σταθερά, καθώς επίσης και την τεταγμένη yB του σημείου Β, ενώ η τετμημένη α του σημείου Β μπορεί να μεταβάλλεται. Η χάντρα διανύει τις διάφορες διαδρομές Α→Β(α)→C με την ίδια αρχική ταχύτητα v_{A}. Να δείξετε ότι η διαδρομή στην οποία η χάντρα κάνει τον ελάχιστο χρόνο να πάει από το Α στο C, ικανοποιεί την εξίσωση του «μηχανικού νόμου Snell» : \frac{\sin \theta_{1}}{\sin \theta_{2}}=\frac{\bar{v}_{1}}{\bar{v}_{2}} , όπου \theta_{1} και  \theta_{2}, οι γωνίες «πρόσπτωσης» και «διάθλασης», αντίστοιχα.

υπόδειξη:
1. η απάντηση προκύπτει εύκολα εφαρμόζοντας το θεώρημα της μέσης ταχύτητας ή θεώρημα Merton (βλέπε πράσινο ένθετο του κεφαλαίου 1.1 στο βιβλίο της Α’ Λυκείου ΕΔΩ)
2. t_{o \lambda}=\frac{AB}{\bar{v}_{1}}+\frac{BC}{\bar{v}_{2}} . Εκφράζουμε τις (υποτείνουσες ορθογωνίων τριγώνων) ΑΒ και BC συναρτήσει της μεταβλητής α (οι μέσες ταχύτητες δεν εξαρτώνται από την μεταβλητή α), και απαιτούμε η συνάρτηση t_{o \lambda}(a) να έχει ελάχιστο: dt_{o \lambda}(a)/da=0. H απόδειξη είναι παρόμοια με την απόδειξη του νόμου διάθλασης του Snell εφαρμόζοντας την αρχή του Fermat.

… περισσότερα θα βρείτε εδώ: «Mechanical Snell’s Law»
https://arxiv.org/pdf/2012.08062.pdf

(νεώτερη ενημέρωση 17/11/2025)
Διαβάστε επίσης: Πότε θα φτάσει συντομότερα;

‹
›

Κατηγορίες:ΜΑΘΗΜΑΤΙΚΑ, ΜΗΧΑΝΙΚΗ

Ετικέτες: , , ,

2 replies

  1. George Metaxas's avatar
    George Metaxas
    17/11/2025 • 2:08 μμ

    Μία ενδιαφέρουσα οπτικοποίηση στην καμπύλη εκδοχή του πειράματος (προσέξτε τον τίτλο «Brachystochrone Curve»): https://www.youtube.com/watch?v=TIopneBToLQ&t=2s

    Reply ↓

Σχολιάστε

Ο ιστότοπος χρησιμοποιεί το Akismet για την εξάλειψη των ανεπιθύμητων σχολίων. Μάθετε πως επεξεργάζονται τα δεδομένα των σχολίων σας.