Σύμφωνα με τον Ν. David Mermin (βλέπε Είναι θέμα χρόνου), «… συχνά αναφερόμαστε στην επιβράδυνση των κινούμενων ρολογιών χρησιμοποιώντας τον πραγματικά αξιοθρήνητο όρο ‘διαστολή του χρόνου’. Ακούγομαι τόσο απαξιωτικός γιατί ο συγκεκριμένος όρος προτείνει με εντελώς ασαφή τρόπο ότι ‘ο χρόνος ο ίδιος’ – ό,τι και να σημαίνει αυτό – είναι αυτός που διαστέλλεται όταν ένα κινούμενο ρολόι πάει αργά. Κι ενώ η αντίληψη ότι ο χρόνος ‘απλώνει’ για ένα συγκεκριμένο κινούμενο ρολόι αποτελεί μία πιο ενστικτώδη προσέγγιση στο θέμα, είναι σημαντικό να καταλάβουμε ότι αυτό στο οποίο αναφερόμαστε δεν έχει να κάνει με την πρωταρχική έννοια του χρόνου. Αποτελεί απλά μια σχέση μεταξύ δυο συνόλων ρολογιών.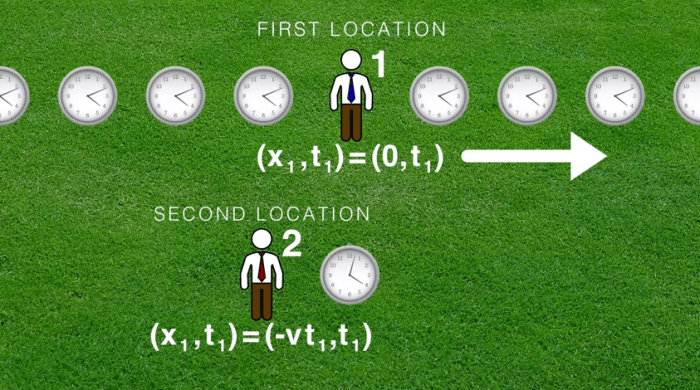 Παρόλο που όλοι πιστεύουμε ότι ο χρόνος υφίσταται και ότι μετριέται με τη χρήση ρολογιών, ένα από τα μεγαλύτερα μαθήματα της σχετικότητας είναι ότι η έννοια του χρόνου δεν είναι τίποτε παραπάνω από μία βολική και εύκολη σύμβαση, αν και δυνητικά δόλια και επικίνδυνη που συνοψίζει συμπαγώς όλες τις σχέσεις που υπάρχουν μεταξύ διαφορετικών ρολογιών.
Παρόλο που όλοι πιστεύουμε ότι ο χρόνος υφίσταται και ότι μετριέται με τη χρήση ρολογιών, ένα από τα μεγαλύτερα μαθήματα της σχετικότητας είναι ότι η έννοια του χρόνου δεν είναι τίποτε παραπάνω από μία βολική και εύκολη σύμβαση, αν και δυνητικά δόλια και επικίνδυνη που συνοψίζει συμπαγώς όλες τις σχέσεις που υπάρχουν μεταξύ διαφορετικών ρολογιών.
Αν ένα σύνολο ρολογιών (1) που θεωρούνται ακίνητα και συγχρονισμένα τρέχουν με τον σωστό ρυθμό, τότε ένα δεύτερο σύνολο ρολογιών (2) που θεωρούνται κινούμενα – και συγχρονισμένα στο σύστημα αναφοράς στο οποίο τα ρολόγια αυτά είναι ακίνητα – αποδεικνύονται εκτός συγχρονισμού και ότι πάνε με αργό ρυθμό, σύμφωνα με το πρώτο σύνολο ρολογιών (1).
Αν, όμως, θεωρήσουμε το δεύτερο σύνολο (2) να είναι ακίνητο και τα ρολόγια του συγχρονισμένα στον σωστό ρυθμό, τότε βρίσκουμε το πρώτο σύνολο των ρολογιών (1) να είναι εκτός συγχρονισμού και ότι πάνε με αργό ρυθμό, σύμφωνα με το δεύτερο σύνολο ρολογιών (2).
Παρατηρείται λοιπόν διάσταση απόψεων ως προς τα συμπεράσματα. Πως μπορεί ο παρατηρητής 1 να ισχυρίζεται ότι τα ρολόγια του παρατηρητή 2 πάνε πιο αργά, αλλά και ο παρατηρητής 2 να ισχυρίζεται ότι τα ρολόγια του παρατηρητή 1 επίσης πάνε αργά, όταν στην ουσία και οι δυο μιλούν για τα ίδια σύνολα ρολογιών; Αν ο παρατηρητής 1 ισχυρίζεται ότι τα ρολόγια του 2 τρέχουν αργά, δεν πρέπει ο παρατηρητής 2 να ισχυριστεί ότι τα ρολόγια του 1 τρέχουν γρήγορα; …»
Ας δούμε στο βίντεο που ακολουθεί πως εξηγεί ο Don Lincoln αυτό το φαινομενικό παράδοξο:
Κατηγορίες:ΣΧΕΤΙΚΟΤΗΤΑ
Σε όσους κατενόησαν αυτή την ανάρτηση απευθύνω Θερμά Συγχαρητήρια.
Όμως, σε όσους δεν την κατενόησαν, και έχουν το θάρρος να το ομολογήσουν τουλάχιστον στον εαυτό τους, προτείνω να πληκτρολογήσουν στο Google: «Προς Φυσικούς Επιστήμονες».
Διονύσης Γ. Ραυτόπουλος