Ένα κλασικό πρόβλημα που κάποτε αντιμετώπιζαν οι μαθητές της Α’ Λυκείου ήταν το εξής:
Να υπολογιστούν οι χρονικές στιγμές που συμπίπτουν ο ωροδείκτης και ο λεπτοδείκτης ενός ρολογιού από τo μεσημέρι μέχρι τα μεσάνυχτα.
Η απάντηση που δινόταν συνήθως – χρησιμοποιώντας τις έννοιες της περιόδου Τ και της γωνιακής ταχύτητας (ω = θ/t = 2π/Τ) στην ομαλή κυκλική κίνηση -, ήταν κάπως έτσι :
Έστω ότι το ρολόι δείχνει δώδεκα ακριβώς, όπου ο λεπτοδείκτης με τον ωροδείκτη συμπίπτουν.
Αν οι δυο δείκτες συναντώνται μετά από t sec, τότε ο μεν ο ωροδείκτης που κινείται με γωνιακή ταχύτητα ωΩ=2π/ΤΩ rad/s διανύει γωνία θΩ rad, ενώ ο λεπτοδείκτης που κινείται με γωνιακή ταχύτητα ωΛ = 2π/ΤΛ rad/s διανύει γωνία θΛ=θΩ+2π rad.
Δεδομένου ότι η περίοδος του λεπτοδείκτη είναι ΤΛ=1 h, ενώ η περίοδος του ωροδείκτη ΤΩ = 12h, θα έχουμε:
ωΛt= ωΩt +2π και t=TΛ∙ΤΩ/(ΤΛ-ΤΩ) = 12/11 h = 3927,2727 sec ή 1 ώρα και 5 λεπτά και 27,3 δευτερόλεπτα.
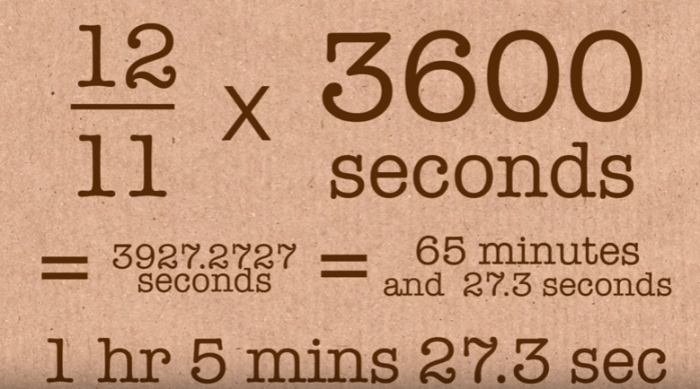
Έτσι, κάθε 3927,2727 δευτερόλεπτα περίπου, ο λεπτοδείκτης και ο ωροδείκτης συναντώνται 11 φορές από τα μεσάνυχτα μέχρι το μεσημέρι της επόμενης μέρας:
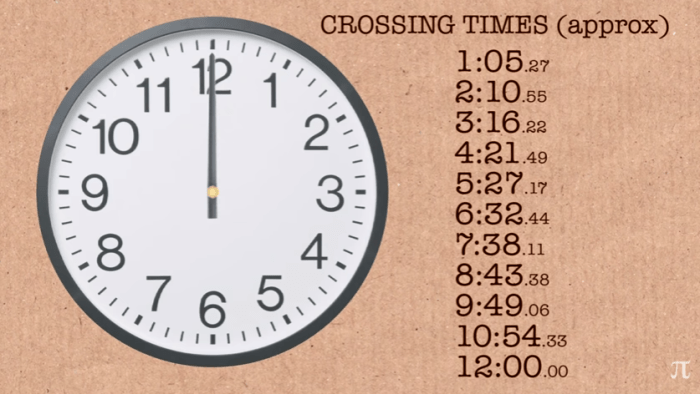 Δεν χρειάζονται βέβαια οι έννοιες της ομαλής κυκλικής κίνησης για να γίνει ο παραπάνω υπολογισμός.
Δεν χρειάζονται βέβαια οι έννοιες της ομαλής κυκλικής κίνησης για να γίνει ο παραπάνω υπολογισμός.
Αρκεί να συνειδητοποιήσει κανείς πως οι δείκτες συναντώνται 11 φορές σε ίσα χρονικά διαστήματα μέσα σε ένα δωδεκάωρο. Τότε προκύπτει αμέσως ότι δυο διαδοχικές συμπτώσεις του λεπτοδείκτη με τον ωροδείκτη συμβαίνουν σε χρονικό διάστημα 12/11 h. Αυτό ακριβώς μας εξηγεί το βίντεο του Numberphile που ακολουθεί:
Κατηγορίες:ΜΑΘΗΜΑΤΙΚΑ, ΜΗΧΑΝΙΚΗ

Εαν ο ωροδεικτης και ο λεπτοδεικτης ειναι στο 12 . ποτε θα σχηματισουν μεταξυ τους γωνια 90 μοιρων για πρωτη φορα