Ένα σχεδόν «μαγικό» πείραμα που μπορεί γίνει πολύ εύκολα είναι το εξής:
Πάρτε ένα μπαλάκι του τένις και τοποθετήστε το πάνω σε μια μπάλα του μπάσκετ. Η μπάλα του μπάσκετ έχει αρκετά μεγαλύτερη μάζα από το μπαλάκι του τένις. Αφήστε τις δυο μπάλες να πέσουν στο πάτωμα προσέχοντας έτσι ώστε η μικρή μπάλα να μην ξεφύγει από την κορυφή της μεγάλης μπάλας. Όταν η μεγάλη μπάλα χτυπήσει στο πάτωμα αντιστρέφει την διεύθυνση της κίνησής της, χωρίς να αλλάξει ταχύτητα, με αποτέλεσμα για ένα πολύ μικρό χρονικό διάστημα η μεγάλη μπάλα να κατευθύνεται προς τα πάνω και η μικρή μπάλα προς τα κάτω με την ίδια ταχύτητα. Αμέσως μετά, η μικρή μπάλα αναπηδά προς τα πάνω με σχεδόν τρεις φορές την αρχική της ταχύτητα. Το ύψος που μπορεί να φτάσει μια μπάλα που κινείται προς τα πάνω είναι ανάλογο του τετραγώνου της αρχικής ταχύτητας της μπάλας, κι αν οι απώλειες λόγω τριβών είναι μικρές, τότε η μικρή μπάλα μπορεί να εκτοξευθεί προς τα πάνω σχεδόν εννιά φορές το ύψος από το οποίο την ρίξαμε αρχικά!
δείτε μια παραλλαγή του πειράματος στο βίντεο «Stacked Ball Drop» (που συσχετίζει το φαινόμενο ακόμα και με την έκρηξη των σουπερνόβα …)
Μια ενδιαφέρουσα και εντυπωσιακότερη παραλλαγή του ίδιου πειράματος φαίνεται στο επόμενο βίντεο από το 7¨59 και μετά:
Το γεγονός ότι μικρή μπάλα (στο πρώτο βίντεο) μετά την κρούση έχει τριπλάσια ταχύτητα από την ταχύτητά της πριν την κρούση μπορεί να εξαχθεί αλγεβρικά, εφαρμόζοντας τις εξισώσεις των ταχυτήτων μετά την ελαστική κρούση, όπως προκύπτουν όταν εφαρμόζουμε τις αρχές διατήρησης της ορμής και ενέργειας:
Αρκεί να θεωρήσουμε ότι οι δύο μάζες (m2>>m1) κινούνται με ταχύτητες ίσου μέτρου αλλά αντίθετης φοράς. Αλλά έτσι μπλέκουμε με μαθηματικές εξισώσεις και πολλές αλγεβρικές πράξεις …
Ευτυχώς υπάρχει ένας απλούστερος τρόπος. Το μόνο που χρειάζεται να γνωρίζουμε ότι όταν μια μπάλα συγκρούεται ελαστικά με μια άλλη μπάλα πολύ μεγαλύτερης μάζας που είναι ακίνητη, η μικρή μπάλα ανακλάται με την ίδια ταχύτητα προς τα πίσω, ενώ η μεγάλη μπάλα παραμείνει ακίνητη (σαν να συγκρούεται ένα μπαλάκι του πιγκ-πογκ με μια ακίνητη μπάλα του μπόουλιγκ). Και κάτι ακόμα. Να χειριζόμαστε την απλούστατη έννοια της σχετικής ταχύτητας.
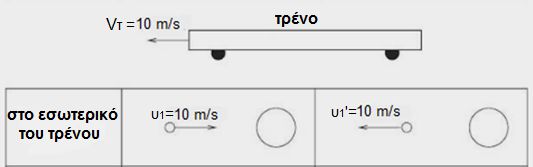
Διαθέτουμε λοιπόν δυο ελαστικές μπάλες – η μία έχει πολύ μεγαλύτερη μάζα από την άλλη (m2>>m1) – και στο σύστημα αναφοράς ενός ευθύγραμμα κινούμενου τρένου με σταθερή ταχύτητα Vτ=10 m/s πραγματοποιείται το εξής πείραμα: η μικρή μπάλα κινείται κατά μήκος του τρένου με ταχύτητα υ1=10 m/s (ως προς το σύστημα αναφοράς του τρένου) και συγκρούεται ελαστικά – μετωπικά με την μεγάλη μπάλα, η οποία είναι ακίνητη (ως προς το τρένο).Όπως είπαμε και προηγουμένως, η μικρή μπάλα απλά θα ανακλαστεί με την ίδια ταχύτητα και η μεγάλη μπάλα θα παραμείνει ακίνητη.
Και γιατί θεωρούμε ότι το πείραμα γίνεται μέσα σε τρένο που κινείται ευθύγραμμα ομαλά με Vτ=10m/s;
Για να απαντήσουμε σε ένα άλλο ερώτημα του οποίου η απάντηση δεν είναι και τόσο προφανής:
Με τι ταχύτητα θα κινηθεί η κάθε μπάλα μετά την ελαστική κρούση, αν η μικρή μπάλα είναι ακίνητη και η μεγάλη μάζα πέφτει πάνω της με ταχύτητα 10 m/s;
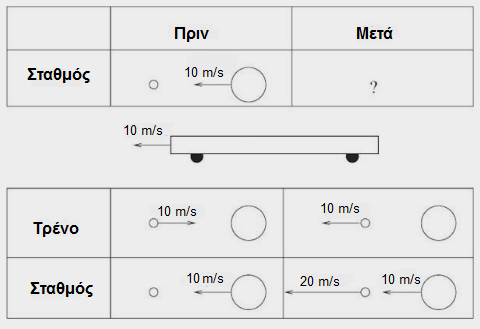
Αν στο προηγούμενο παράδειγμα «μεταφερθούμε» στο σύστημα αναφοράς του σιδηροδρομικού σταθμού, τότε εύκολα διαπιστώνουμε ότι ως προς το σύστημα αυτό, πριν την κρούση η μεγάλη μπάλα κινείται προς τα αριστερά με ταχύτητα 10 m/s, ενώ η μικρή μπάλα είναι ακίνητη.
Τι θα βλέπει ο παρατηρητής στο σύστημα αναφοράς του σιδηροδρομικού σταθμού μετά την κρούση;
Αφού γνωρίζουμε τι συμβαίνει στο σύστημα αναφοράς του τρένου, μπορούμε εύκολα να καταλάβουμε τι θα βλέπει ο παρατηρητής του σταθμού αμέσως μετά την κρούση:Η μικρή μπάλα θα έχει τώρα ταχύτητα 20 m/s και η μεγάλη πάλι 10m/s.
Με λίγα λόγια, αν η μικρή μπάλα είναι αρχικά ακίνητη, τότε μετά την κρούση θα κινείται με την διπλάσια ταχύτητα της μεγάλης μπάλας.
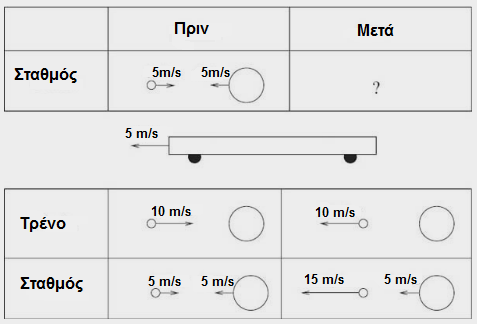
Ένα δεύτερο ενδιαφέρον συμπέρασμα προκύπτει αν θεωρήσουμε πάλι τις δυο μπάλες (η μία πολύ μικρότερης μάζας από την άλλη) και ότι το τρένο κινείται προς την ίδια κατεύθυνση, αλλά με ταχύτητα 5 m/s.
Τότε οι δυο μπάλες – ως προς το σύστημα αναφοράς του σταθμού – φαίνονται να κινούνται πριν την κρούση με αντίθετες ταχύτητες μέτρου 5 m/s.
Στην περίπτωση αυτή, εφαρμόζοντας την ίδια συλλογιστική, μπορούμε να βρούμε αμέσως τις ταχύτητες των δυο μαζών (ως προς το σύστημα αναφοράς του σταθμού): Τώρα η μικρή μάζα θα κινηθεί με ταχύτητα τριπλάσια από την αρχική της. Έτσι εξηγείται και το αποτέλεσμα του εντυπωσιακού πειράματος με τις μπάλες του μπάσκετ και του τένις που αναφέρθηκε στην αρχή της ανάρτησης.
Η συλλογιστική που εφαρμόζουμε εδώ παρουσιάζεται (με περισσότερα παραδείγματα) σε ένα βιβλίο που μας εισάγει με έναν εντυπωσιακά πρωτότυπο τρόπο στην θεωρία της ειδικής σχετικότητας του Αϊνστάιν. Πρόκειται για το βιβλίο του N. David Mermin «Είναι θέμα χρόνου», εκδόσεις ΡΟΠΗ. Ο Mermin στο πρώτο κεφάλαιο προσπαθεί να εξηγήσει την αρχή της σχετικότητας και να εξασκήσει τον αναγνώστη στο να εναλλάσσει την περιγραφή των γεγονότων από την οπτική του ενός συστήματος αναφοράς (π.χ. του τρένου) στην οπτική ενός άλλου συστήματος αναφοράς (π.χ. του σταθμού). Η σχετικότητα, κατά τη γνώμη του Mermin, πρέπει να αποτελεί μέρος της ύλης του λυκείου για δυο βασικούς λόγους: αρχικά, γιατί αποτελεί μια εκπληκτική εφαρμογή των μαθηματικών του λυκείου, αλλά και επειδή όλοι μας, χωρίς να το γνωρίζουμε, είμαστε αρκετά εξοικειωμένοι με την έννοια της σχετικότητας. Γιατί η σχετικότητα έχει να κάνει με τον χρόνο. Τι άλλο θα μπορούσε να μας είναι πιο οικείο; …
Aκολουθεί ο πρόλογος του βιβλίου από τον Θεοχάρη Αποστολάτο (via www.anixneuseis.gr):
«Ακόμα ένα βιβλίο σχετικότητας, λοιπόν, έρχεται να προστεθεί στη μακροσκελή λίστα βιβλίων που έχουν γραφτεί για να βοηθήσουν τον διψασμένο και ενθουσιώδη αναγνώστη να κατανοήσει μια θεωρία που, αν και δεν έχει διαψευστεί έως σήμερα από κανένα πειραματικό αποτέλεσμα, εξακολουθεί να παραμένει μυστηριώδης και δυσνόητη για τους περισσότερους. Ο κυριότερος λόγος αυτής της δυσκολίας σχετίζεται με την αδυναμία των ανθρώπων να συλλάβουν και να αποδεχτούν μια νοητική αφαίρεση που έρχεται σε αντίφαση με τη λογική, όπως αυτή διαμορφώνεται από την καθημερινή εμπειρία τους. Τα φαινόμενα που πραγματεύεται η ειδική θεωρία της σχετικότητας και τα συμπεράσματα στα οποία αυτή καταλήγει δεν συνάδουν με την επικρατούσα αντίληψη για τον κόσμο γύρω μας.
Τα βιβλία που έχουν στόχο να εισαγάγουν τον αμύητο αναγνώστη στην ειδική θεωρία της σχετικότητας είτε παρουσιάζουν τις αρχές και τα αποτελέσματα της θεωρίας, βλέποντάς τα με μια φρέσκια ματιά, είτε τροποποιούν τη σειρά με την οποία αυτά παρουσιάζονται με κριτήριο την ιεράρχηση που ικανοποιεί την επιστημονική θεώρηση του συγγραφέα.
Στο χρονικό διάστημα που μεσολάβησε από τη διατύπωση της ειδικής θεωρίας της σχετικότητας, από το 1905 έως σήμερα, εξαιρετικοί φυσικοί, συμπεριλαμβανόμενου και του ίδιου του Αϊνστάιν, ανταποκρίθηκαν στην πρόκληση και αποπειράθηκαν να γράψουν κάποιο βιβλίο σχετικότητας, εκλαϊκευτικό ή μη. Οι πιθανότητες, επομένως, να γραφτεί κάτι πραγματικά καινούριο, έστω και από αισθητικής πλευράς, έχουν αρχίσει να μειώνονται απελπιστικά.
Ευτυχώς η δημιουργικότητα του ανθρώπινου νου είναι αστείρευτη και η παραπάνω απαισιόδοξη άποψη δεν μπορεί να έχει απόλυτη ισχύ. Το βιβλίο του David Mermin «It’s About Time» αποτελεί μία ειδική περίπτωση βιβλίου σχετικότητας. Ομολογώ ότι άρχισα να το διαβάζω, πιστεύοντας ότι μέσα στις σελίδες του δεν θα έβρισκα τίποτε άλλο παρά μία ακόμα παρουσίαση της ειδικής θεωρίας της σχετικότητας διατυπωμένη, στην καλύτερη περίπτωση, με προσοχή και σαφήνεια. Ωστόσο, σύντομα διαπίστωσα ότι κρατούσα στα χέρια μου τη μεστή εμπειρία ενός δασκάλου που έχει πασχίσει να διατυπώσει προτάσεις αφενός μεν επιστημονικά ορθές, αφετέρου δε αφομοιώσιμες από ένα ακροατήριο που δεν έχει επιστημονική καλλιέργεια αλλά διαθέτει ορθή λογική σκέψη και επιθυμεί να κατανοήσει κάτι τόσο δυσνόητο όσο η ειδική θεωρία της σχετικότητας.
Θα πρόσθετα επίσης ότι ο Mermin έχει «ζυμώσει» τη θεωρία της σχετικότητας πολύ καλά. Τα αποτελέσματα αυτής της ζύμωσης είναι εντυπωσιακά. Κατάφερε να επαναδιατυπώσει σε μία μορφή γυμνασιακή από πλευράς μαθηματικών, εξαιρετικά όμως περιεκτική και πλήρως κατανοητή, προτάσεις που συνήθως εμφανίζονται στα βιβλία ενδεδυμένες με περίτεχνη μαθηματική φόρμα, αλλά ουσιαστικά δυσνόητες.
Το κείμενο του David Mermin διαθέτει την απλότητα του τρόπου με τον οποίο ο ίδιος ο Αϊνστάιν γράφει το περίφημο άρθρο του, το 1905, όταν σε νεαρή ακόμα ηλικία παρουσιάζει απλά, με ύφος σχεδόν παιδαριώδες, τις αρχές της ειδικής θεωρίας της σχετικότητας, προκειμένου να καταφέρει να «στήσει» τον ηλεκτρομαγνητισμό στο μοναδικό φυσικό πλαίσιο στο οποίο αυτός αποκτά νόημα: το σχετικιστικό. Θα μπορούσε κανείς να υποστηρίξει ότι η γλώσσα που χρησιμοποιεί στο βιβλίο του ο Mermin δεν είναι επιστημονική αλλά απλή καθημερινή γλώσσα, και επομένως το ανάγνωσμα αυτό δεν έχει καμία θέση στη βιβλιοθήκη κάποιου φυσικού ή επιστήμονα. Μια τέτοια άποψη, κατά τη γνώμη μου, είναι απολύτως αφελής. Εκείνος που έχει καταφέρει να εξηγήσει με εύκολο και ανεπιτήδευτο λόγο κάτι τόσο δύσκολο να συλλάβει ο κοινός νους έχει κατορθώσει κάτι πολύ σπουδαίο· έχει εντοπίσει τον πραγματικό λόγο της δυσκολίας και έχει εστιάσει στις απαιτητικές έννοιες, τις οποίες καταφέρνει τελικά να εξηγήσει με απλότητα και απόλυτη σαφήνεια.
Είμαι σίγουρος ότι ο Mermin έχει βασανιστεί σκληρά και για μεγάλο χρονικό διάστημα για να υλοποιήσει τον εξαιρετικά δύσκολο στόχο του. Αυτός, όμως, είναι και ο ρόλος του αληθινού δασκάλου και επιστήμονα: να κατορθώσει να φέρει σε αρμονική σύζευξη το γνωστικό του αντικείμενο με τους νευρώνες του εγκεφάλου των μαθητών του.
Πιστεύω ότι αυτός που θα διαβάσει προσεκτικά το βιβλίο του Mermin θα αποδεχτεί τελικά ως απολύτως λογική την αλλαγή του ρυθμού ροής του χρόνου σε διαφορετικά συστήματα αναφοράς. Στη συνέχεια τα εκ πρώτης όψεως παράδοξα φαινόμενα της διαστολής του χρόνου και της συστολής του μήκους αρχίζουν να αναδεικνύονται ως απολύτως λογικά και αναμενόμενα επακόλουθα του πειραματικού αποτελέσματος που επιβεβαιώνει ότι η ταχύτητα του φωτός είναι παγκόσμια και απόλυτη.
Παρόλο που για έναν ώριμο φυσικό με καλή γνώση της σχετικότητας είναι μεγάλη απόλαυση να παρακολουθεί τον Mermin να αποκαθηλώνει και να ξαναστήνει με στέρεο τρόπο και συνάμα κομψότατο στιλ το οικοδόμημα που έχει στο μυαλό του, το βιβλίο του δεν είναι ένα ανάγνωσμα που διαβάζεται στην παραλία. Είναι αρκετά απαιτητικό και ο αναγνώστης χρειάζεται να καταβάλει προσπάθεια για να παρακολουθήσει απρόσκοπτα τη ροή των επιχειρημάτων του συγγραφέα. Δεν πρόκειται, όμως, να κουραστεί. Ο συγγραφέας, διατηρώντας μέσα στις σελίδες του βιβλίου του μία λεπτή αίσθηση του χιούμορ, φροντίζει να ξεκουράζει τον αναγνώστη χωρίς, όμως, να του επιτρέπει να χαλαρώσει. Σύντομα τον επαναφέρει σε κατάσταση εγρήγορσης και τον καλεί να εκτελέσει τους υπολογισμούς, ακολουθώντας τις υποδείξεις του, ώστε να βιώσει και αυτός την αίσθηση της ανακάλυψης. Ο δάσκαλος που έχει γνωρίσει τη γλυκύτατη αυτή αίσθηση είναι αρκετά γενναιόδωρος, ώστε να θέλει να τη μοιραστεί με τους μαθητές του.
Συγκρίνοντας το βιβλίο του Mermin με άλλα πολύ καλά βιβλία, όπως αυτό των Taylor και Wheeler «Spacetime Physics» που απευθύνεται επίσης σε μη φυσικούς (ή τουλάχιστον σε μη ώριμους φυσικούς), διαπιστώνουμε ότι ο Mermin καινοτομεί, όταν αποφασίζει να μην χρησιμοποιήσει την παιδαγωγική μέθοδο της αναλογίας, μια μέθοδο την οποία εγώ ο ίδιος αγαπώ ιδιαίτερα. Δεν προσπαθεί να πείσει τον αναγνώστη ότι έχει κατανοήσει τις βαθύτερες έννοιες που του εξηγεί μέσω κάποιου παραδείγματος το οποίο γίνεται άμεσα αντιληπτό και «ερμηνεύει» με τις κατάλληλες αναλογίες αυτό που δεν «χωράει», ως έχει, στο μυαλό του αμύητου. Υποθέτω ότι θεωρεί επικίνδυνη μια τέτοια ενέργεια. Η χρήση αναλογιών, όσο δημιουργική και ευφυής και αν είναι, μπορεί να αποβεί παραπειστική και εν τέλει διαστρεβλωτική. Όποιος δεν έχει μάθει να χειρίζεται τις αναλογίες με την κατάλληλη επιφύλαξη και προσοχή ενδέχεται να οδηγηθεί σε αυθαίρετα συμπεράσματα, τα οποία ουδεμία σχέση έχουν με την πραγματικότητα. Μου έχει τύχει να ακούσω ανθρώπους που διαβάζουν εκλαϊκευτικά επιστημονικά βιβλία να «εξηγούν» τον κόσμο μας με οικοδομήματα από «up quarks» που κάθονται πάνω σε «down quarks» σχηματίζοντας τους πυρήνες των ατόμων… Προκειμένου, λοιπόν, να αποφύγει αυθαίρετες παρεξηγήσεις, ο Mermin ακολουθεί τον δρόμο των άμεσα μετρήσιμων ποσοτήτων και με αφετηρία κάποιες πρωταρχικές ποσότητες, τις οποίες φροντίζει πρώτα να εξηγήσει και να διασαφηνίσει όσο πληρέστερα γίνεται, χτίζει κατόπιν όλες τις άλλες.
Υπάρχει και άλλη μία πιο κρυφή πτυχή στα κεφάλαια του βιβλίου του Mermin. Η φυσική θα έλεγε κανείς ότι αποτελεί ένα αυστηρό και λιτό σύνολο το οποίο δομείται ιεραρχικά από τα θεμέλια μέχρι τις επί μέρους μικρές λεπτομέρειές του. Η αλήθεια είναι ότι στο σύνολό της η φυσική παρουσιάζει εξαιρετικές διασυνδέσεις φαινομενικά άσχετων εννοιών και μεθόδων ανάλυσης. Όλα τα στοιχεία αυτού του αυστηρού, δωρικού οικοδομήματος αλληλεπιδρούν μεταξύ τους, σαν να επρόκειτο για μέλη ενός ζωντανού οργανισμού. Ο Mermin, είτε συνειδητά είτε ασυνείδητα, αφήνει στο βιβλίο του να διαφανεί αυτή η εσωτερική διαλεκτική στη σχετικότητα, όταν υπολογίζοντας μια ποσότητα προκειμένου να οδηγηθεί σε κάποιο συμπέρασμα μας εξηγεί ότι το αποτέλεσμα του υπολογισμού θα μπορούσε να έχει προκύψει εναλλακτικά μέσα από κάποια άλλη σύνδεση ποσοτήτων που έχουν εμφανιστεί σε προηγούμενο κεφάλαιο. Αυτή η εσωτερική συνοχή και αλληλεξάρτηση που ενυπάρχει στη φυσική χαρίζει στο όλο δημιούργημα μία κρυφή γοητεία που οι μυημένοι γνωρίζουν καλά. Μπορεί το συλλογικό οικοδόμημα της φυσικής να γεννά στις ψυχές των αμύητων δέος, αλλά η εσωτερική συνοχή είναι αυτή που πραγματικά μαγεύει τον εργάτη της επιστήμης.
Το βιβλίο που κρατάτε στα χέρια σας, εκτός του ότι είναι απλό και διδακτικό, είναι συνάμα και γοητευτικό. Διακρίνεται για την καθαρότητα του λόγου και τη σαφήνεια των προβληματισμών και των απαντήσεων που δίνει. Εγώ προσωπικά, έχοντας διαβάσει το βιβλίο «It’s About Time», αισθάνομαι ότι βρήκα μία νέα πηγή έμπνευσης για το μάθημα της Ειδικής Σχετικότητας που διδάσκω στους εκκολαπτόμενους φυσικούς του Πανεπιστημίου Αθηνών.
Κατηγορίες:ΕΚΠΑΙΔΕΥΣΗ, ΜΗΧΑΝΙΚΗ, ΣΧΕΤΙΚΟΤΗΤΑ
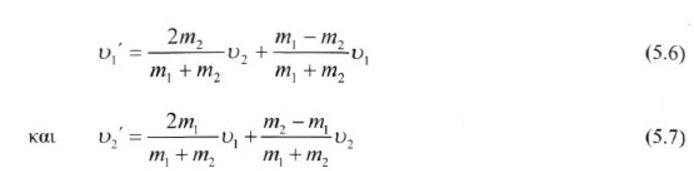

Σχολιάστε