Αρχική › ΒΑΡΥΤΗΤΑ › Βαρυτική ερυθρή μετατόπιση και το πείραμα Pound-Rebka

Βαρυτική ερυθρή μετατόπιση και το πείραμα Pound-Rebka

By on • ( 7 )

Η βαρυτική ερυθρή μετατόπιση ήταν μια από τις πρώτες μεγάλες προβλέψεις του Αϊνστάιν. Έγινε το 1907, οκτώ χρόνια από την τελική διατύπωση της γενικής σχετικότητας. Παραδόξως όμως, αυτή η πρόβλεψη ήταν η τελευταία που ελέγχθηκε με αξιόλογη ακρίβεια.

O Glen Rebka στο κάτω άκρο του πύργου Jefferson στο πανεπιστήμιο του Harvard

O Glen Rebka στο κάτω άκρο του πύργου Jefferson στο πανεπιστήμιο του Harvard εκτελεί πειράματα σχετικά με την βαρυτική ερυθρή μετατόπιση φωτός στο πεδίο βαρύτητας της Γης

Το κβάντο του φωτός, το φωτόνιο, έχει ενέργεια E = hf ,
όπου h η σταθερά του Planck και f η συχνότητα,
Σύμφωνα με την ισοδυναμία μάζας–ενέργειας E = m c^{2} , το φωτόνιο θα έχει και μάζα μ :
hf = \mu c^{2} \Rightarrow \mu = hf/c^{2}
Εξαιτίας της μάζας αυτής, το φως θα επηρεάζεται από το πεδίο βαρύτητας, γεγονός που έχει σχέση με την ερυθρή βαρυτική μετατόπιση του φωτός, ένα φαινόμενο που αποδείχθηκε με ακρίβεια πειραματικά για πρώτη φορά το 1959, επιβεβαιώνοντας για άλλη μια φορά τις προβλέψεις του Einstein.

Για να γίνει κατανοητή η βαρυτική μετατόπιση, φανταζόμαστε μια πηγή φωτός με καλά ορισμένη συχνότητα ή μήκος κύματος, που είναι τοποθετημένη στην κορυφή ενός ψηλού πύργου και εκπέμπει φως προς τα κάτω.
Ένας ρυθμιζόμενος δέκτης τοποθετείται στο έδαφος και ρυθμίζεται έτσι ώστε να λάβει το σήμα από την πηγή πάνω στον πύργο.
Αν συγκρίνουμε τη συχνότητα του λαμβανόμενου σήματος με εκείνη του εκπεμπόμενου, αυτή θα είναι μεγαλύτερη, μικρότερη ή η ίδια;
σχημα1Η «πτώση του φωτός» και το πείραμα Pound–Rebka

Εφόσον το φωτόνιο που εκπέμπεται προς τα κάτω, από την κορυφή ενός κτιρίου ύψους H , έχει μάζα \mu = hf/c^{2} ,
θα φτάσει στο έδαφος με μεγαλύτερη «εσωτερική ενέργεια» (άρα και συχνότητα)
αφού η βαρυτική δυναμική ενέργεια \mu g H που είχε αρχικά θα μετατραπεί και αυτή σε «εσωτερική ενέργεια» του φωτονίου σύμφωνα με τη σχέση
hf + \mu g H = h f'
ή δεδομένου ότι \mu = hf/c^{2}
f'=f(1+ gh/c^{2}) \, \, \, \, (1)
Για «πτώση» από ύψος, π.χ. Η=100m, η ποσοστιαία αλλαγή συχνότητας \Delta f/f = gH/c^{2} είναι της τάξεως του 10-11 και τέτοιες μεταβολές συχνότητας μετρήθηκαν για πρώτη φορά με αξιόλογη ακρίβεια το 1959 από το πείραμα των Pound-Rebka.

Στο πείραμα χρησιμοποιήθηκε ο πύργος Jefferson του κτιρίου φυσικής στο πανεπιστήμιο του Harvard. Για τo ύψος του πύργου, περίπου 23 μέτρα, η προβλεπόμενη μετατόπιση στη συχνότητα είναι μόλις δυο μέρη στο τετράκις εκατομμύριο. Για να γίνει το πείραμα απαιτείται πομπός και δέκτης με εξαιρετικά καλά ορισμένη συχνότητα.

Μια τέτοια δυνατότητα δίνεται από την διεγερμένη κατάσταση του πυρήνα του ισοτόπου 57Fe, η οποία έχει χρόνο ημιζωής ένα δέκατο του ενός εκατομμυριοστού του δευτερολέπτου.

iron57Από την αποδιέγερση αυτού του ισοτόπου προκύπτουν ακτίνες γ, ενέργειας 14,4 KeV ή μήκους κύματος 0,086 νανόμετρα, μέσα σε μια πολύ στενή ζώνη μηκών κύματος, πλάτους ενός τρισεκατομμυριοστού του βασικού μήκους κύματος. Το ίδιο ισότοπο μπορεί επίσης να απορροφήσει ακτίνες γ του ίδιου μήκους κύματος στην ίδια στενή ζώνη.

Όμως από μόνο του αυτό δεν αρκεί για να μετρηθεί η ερυθρή μετατόπιση. Μέσα σε κάθε πραγματικό δείγμα που περιέχει πυρήνες 57Fe, οι πυρήνες του σιδήρου βρίσκονται σε διαρκή κίνηση λόγω της θερμικής τους ενέργειας.

Τούτο προκαλεί μετατοπίσεις Doppler στις εκπεμπόμενες συχνότητες των ακτίνων γ, με αποτέλεσμα να διευρύνεται η ζώνη συχνοτήτων.

Επιπλέον, όταν ο πυρήνας του σιδήρου εκπέμψει ή απορροφήσει ακτίνες γ υφίσταται ανάκρουση, και η ταχύτητα ανάκρουσης προκαλεί επίσης μια μετατόπιση Doppler στη συχνότητα.

Τα φαινόμενα αυτά μπορούν να διευρύνουν την ζώνη των συχνοτήτων του 57Fe τόσο πολύ, ώστε θα ήταν αδύνατον να μετρηθεί η βαρυτική ερυθρή μετατόπιση, αν δεν υπήρχε ο Rudolf Mössbauer.

Στα τέλη της δεκαετίας του 1950, ο Mössbauer ανακάλυψε ότι αν εμφυτεύσουμε έναν τέτοιο πυρήνα μέσα σε κατάλληλο είδος κρυστάλλου, τότε οι δυνάμεις που ασκούν πάνω του τα άλλα άτομα που τον περιστοιχίζουν, όχι μόνο περιορίζουν τις θερμικές ταλαντώσεις του πυρήνα, αλλά επίσης μεταβιβάζουν στο κρύσταλλο ως όλον την ορμή ανάκρουσης του εκπέμποντος πυρήνα.

Με αυτόν τον τρόπο εξαλείφεται εν δυνάμει η ταχύτητα ανάκρουσης του πυρήνα. Γι την ανακάλυψη αυτή ο Mössbauer βραβεύθηκε με το Νόμπελ φυσικής το 1961.

Οι Pound και Rebka χρησιμοποίησαν το φαινόμενο Mössbauer στο πείραμά τους προκειμένου να κατασκευάσουν πομπούς και δέκτες ακτίνων γ με εξαιρετικό εύρος συχνοτήτων. Παρ’ όλα αυτά το εύρος των συχνοτήτων του 57Fe ήταν 1000 φορές μεγαλύτερο από το αναμενόμενο μέγεθος της μετατόπισης που έπρεπε να μετρηθεί!

Για να μπορέσουν να μετρήσουν την ζητούμενη μετατόπιση τοποθέτησαν τον πομπό σε μια κινητή πλατφόρμα. Αν ο πομπός βρισκόταν στην κορυφή του πύργου, έτσι ώστε οι ακτίνες γ να έφταναν στη βάση μετατοπισμένες προς το κυανό, τότε ανέβαζαν σιγά- σιγά την πλατφόρμα, προκαλώντας μια μετατόπιση Doppler προς το ερυθρό.
harvtower1
Ρυθμίζοντας την ταχύτητα ανόδου του πομπού οι Pound και Rebka, παρήγαγαν μια ερυθρή μετατόπιση Doppler η οποία αντιστάθμιζε τη βαρυτική κυανή μετατόπιση.

Με τον τρόπο αυτόν, η ζώνη συχνοτήτων των ακτίνων γ που έφταναν στο έδαφος συνέπιπτε αρκετά με τη ζώνη απορρόφησης του δέκτη. Η προς τούτο απαιτούμενη μετατόπιση Doppler έδινε λοιπόν το μέτρο της βαρυτικής κυανής μετατόπισης.

Η απαραίτητη ταχύτητα ήταν περίπου δυο χιλιοστά του μέτρου ανά ώρα. Για να εξαλειφθούν κάποιες πηγές σφάλματος, το πραγματικό πείραμα ήταν συμμετρικό: Οι μισές μετρήσεις έγιναν με έναν πομπό στην κορυφή και έναν δέκτη στο έδαφος, για να μετρηθεί η κυανή μετατόπιση, και άλλες μισές με έναν στο έδαφος και έναν δέκτη στην κορυφή του πύργου, για να μετρηθεί η ίση και αντίθετη ερυθρή μετατόπιση.

Τα αποτελέσματα του πειράματος συμφωνούσαν με την προβλεπόμενη τιμή με περιθώριο σφάλματος 10%, ενώ τα αποτελέσματα μιας βελτιωμένης εκδοχής του πειράματος, που έγινε το 1965 από τον Pound και τον Joseph L. Snider, μείωσαν το σφάλμα στο 1%

Βαρυτική ερυθρή μετατόπιση και ακτίνα Schwarzchild

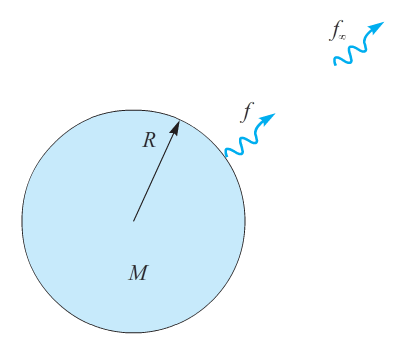
σχήμα2
Η απομάκρυνση ενός φωτονίου από την επιφάνεια ενός άστρου οδηγεί σε μείωση της συχνότητάς του σύμφωνα με την εξίσωση διατήρησης ενέργειας
hf - G \frac{\mu M}{R} = h f_{\infty}
αντικαθιστώντας την μάζα του φωτονίου με \mu = hf/c^{2} παίρνουμε
f_{\infty} = f(1- gR/c^{2}) \, \, \, \, (2)
από την οποία προκύπτει ότι η ποσοστιαία αλλαγή συχνότητας
\Delta f/f = (f - f_{\infty}) = gR/c^{2}
είναι τώρα πολύ μεγαλύτερη, αφού τόσο το g (η επιτάχυνση της βαρύτητας στην επιφάνεια του άστρου) όσο και το R είναι τώρα πολύ μεγαλύτερη, αφού τόσο το g (επιτάχυνση της βαρύτητας στην επιφάνεια του άστρου) όσο και το R είναι τώρα κατά πολλές τάξεις μεγέθους μεγαλύτερα από τις αντίστοιχες ποσότητες στην εξίσωση (1).
Από την (2) – με g = GM/R^{2} – προκύπτει επίσης ότι η συχνότητα του φωτονίου στο άπειρο, η f_{\infty} θα γίνει αρνητική – και άρα η διαφυγή του δεν θα είναι δυνατή – όταν η ακτίνα R του αστρικού αντικειμένου γίνει μικρότερη από την τιμή
R_{0} = GM/c^{2} \, \, \, \, (3)
που είναι γνωστή ως ακτίνα Schwarzchild και είναι βεβαίως η ακτίνα κάτω από την οποία το αστρικό σώμα μετατρέπεται σε μαύρη τρύπα.

ΠΗΓΕΣ:
1. «Εισαγωγή στην Κβαντική Φυσική», Διδάσκων: Σ. Τραχανάς, e- Φυσική στο Πανεπιστήμιο Κρήτης
2. «Είχε δίκιο ο Αϊνστάϊν;», Clifford M. Will, Πανεπιστημιακές Εκδόσεις Κρήτης

‹
›

Κατηγορίες:ΒΑΡΥΤΗΤΑ, ΠΥΡΗΝΙΚΗ ΦΥΣΙΚΗ, ΣΧΕΤΙΚΟΤΗΤΑ

Ετικέτες: , , ,

7 replies

  1. Nick Mastro
    20/10/2015 • 1:08 μμ

    Απλά ρωτάω , αν υπάρχει μια ξεκάθαρη λύση στο εξής πρόβλημα , από την μεριά της ΓΘΣ.Τα φωτόνια δεν έχουν μάζα , αλλά έχουν ενέργεια , και για αυτό το βαρυτικό πεδίο επιδρά πάνω τους και τους αλλάζει τροχιά.Στην ΓΘΣ τα βαρυτόνια ή κύματα βαρύτητας δεν επηρεάζοντε από το πεδίο βαρύτητας?Αυτή γενικά είναι η ερώτηση μου.Προφανώς θα πρέπει να επηρεάζοντε.Ας πούμε ότι τα κβαντικά φαινόμενα δεν παιζουν ρόλο.Γιατί τα φωτόνια δεν πάνε μακρύτερα απο το Rs (ακτίνα schwarzschild) , ενώ τα βαρυτόνια πάνε στο άπειρο?

    Reply ↓
  2. Nick Mastro
    20/10/2015 • 9:19 μμ

    Ευχαριστώ , αλλά δεν κατάλαβα κάτι περισσοτέρο.Το μόνο που κατάλαβα είναι ότι χρειαζόμαστε την κβαντική βαρύτητα.Δηλαδή για να καταλάβω…Η βαρύτητα επιδρά στα φωτόνια , και έχουμε ερυθρά μετατόπιση , ενώ στα κύματα βαρύτητας δεν επιδρά, σωστά???
    Κάτι χάνω!Thanks!

    Reply ↓
  3. pu2keqiri
    22/10/2015 • 3:39 μμ

    Nick Mastro,

    Συνήθως ερώτηματα σαν αυτά μπορούν να τεθούν απλά για dark stars στην Νευτώνεια μηχανική, αγνοώντας έτσι την σχετικότητα. Η GR μας πληροφορεί πως τα βαρυτικά κύματα είναι μη-γραμμικής φύσεως επομένως πράγματι αλληλεπιδρούν και μεταξύ τους δημιουργώντας έτσι ένα ‘πεδίο βαρύτητας για την βαρύτητα’ (δανείζομαι τον όρο από εδώ: http://www.einstein-online.info/spotlights/gravity_of_gravity). Υπάρχει μάλιστα στενή σχέση (Strominger et al.) μεταξύ των EFE και των εξ. Navier-Stokes, γεγονός που αντανακλά την πολυπλοκότητα του προβλήματος ιδωμένο από την σκοπιά του υδροδυναμικού μοντέλου μιας μελανής οπής λόγω της ολογραφίας στον ορίζοντα. Η βαρύτητα δεν είναι φυσικά επανακανονικοποίησιμη σε μια QFT με καμπύλο χωρόχρονο καθώς υπάρχουν απειρισμοί όταν υπολογίζει κανείς loop diagrams ανωτέρας τάξεως στην σκέδαση (virtual) βαρυτονίων. Υπό αυτή την έννοια χρειάζεται μια θεωρία κβαντικής βαρύτητας για να μάθουμε περισσότερα.

    Reply ↓
  4. Χάρης Βάρβογλης
    23/10/2015 • 7:44 πμ

    Ίσως απλούστερα: η Γενική Θεωρία Σχετικότητας ΔΕΝ είναι συμβατή με την Κβαντομηχανική, με εξαίρεση την περιγραφή του φαινομένου της ακτινοβολίας μιας μελανής οπής. Επομένως δεν μπορούμε ΠΑΝΤΑ να απαντάμε σε ερωτήματα που «ανακατεύουν» κβαντικά φαινόμενα με την καμπύλωση του χωροχρόνου, μέχρι να βρούμε την κατάλληλη θεωρία.

    Reply ↓
  5. Nick Mastro
    23/10/2015 • 2:28 μμ

    Σας ευχαριστώ pu2keqiri , Χάρης Βάρβογλη για τις ιδέες σας , επί του θέματος.Αν δείτε στην ανάρτηση αυτό που χρησιμοποιήται είναι η <<Αρχή διατηρήση της Ενέργειας>> , για τον υπολογισμό στο <<Άπειρο >> της συχνότητας του φωτονίου που απομακρύνετε από το βαρυτικό πεδίο , και παρουσιάζει ερυθρή μετατόπιση.Στην αντίθετη περίπτωση το φωτόνιο κερδίζει ενέργεια από το βαρυτικό πεδίο και παρουσιαζει κυανή μετατόπιση.Τώρα ο όρος Μαύρη Οπή είναι απόρεια ότι το φως (Η/Μ ακτινοβολία ) δεν απομακρύνετε από τό σημείο άπειρης πυνκότητας απόσταση μεγαλύτερη από το Rs.ακτίνα Schwarzchild , σχέση (3) .Παρατηρήστε ότι η σχέση (3) είναι το μισό της ακτίνα Schwarzchild που προκύπτει από την ΓΘΣ , αλλά η τάξη μεγέθους είναι μέσα στα όρια.Με δοδομένο οτι η <<Αρχή διατηρήση της Ενέργειας>> θα πρέπει να ισχύει και για τα υποθετικά σωμάτια <<βαρυτόνια>> ή κύματα βαρύτητας, δεν μιλάω για <<εικονικά φωτόνια>> ή για <<εικονικά βαρυτόνια >> , άλλωστε το νέφος των <<εικονικών φωτονίων>> δεν μπορούμε να τα δούμε , ούτε να τα παρατηρήσουμε άμεσα , έτσι έχω καταλάβει, αν έχω λάθος στην κατανόηση των <<εικονικών φωτονίων>> παρακάλώ διορθώστε με , θα έπρεπε να μπορέσουμε να φτάσουμε σε μια αντίστοιχη σχέση για τα <<βαρυτόνια ή κύματα βαρύτητας>>.
    Αν δεν μπορούμε ν’ απαντήσουμε σε αυτό το ερώτημα , εφαρμόζοντας την <<Αρχή διατηρήση της Ενέργειας>> , κάπου υπάρχει BUG στον τρόπο που κατανοουμε και περιγράφουμε την φύση, δεν νομίζετε??
    Σας ευχαριστώ.

    Reply ↓

Σχολιάστε

Ο ιστότοπος χρησιμοποιεί το Akismet για την εξάλειψη των ανεπιθύμητων σχολίων. Μάθετε πως επεξεργάζονται τα δεδομένα των σχολίων σας.