Ένα μαθηματικό πρόβλημα με φυσική σημασία
Ο όγκος της n-διάστατης μοναδιαίας σφαίρας δίνεται από τον τύπο
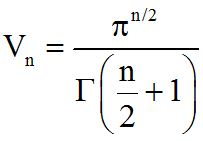 Χρησιμοποιώντας τον τύπο του Stirling για τη συνάρτηση Γάμμα βλέπει κανείς ότι :
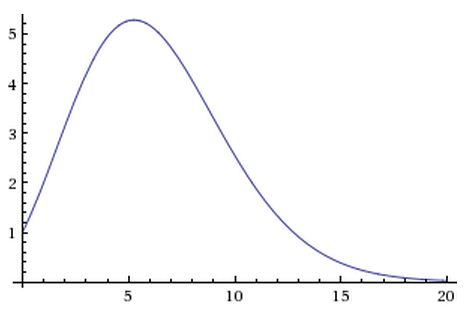
Χρησιμοποιώντας τον τύπο του Stirling για τη συνάρτηση Γάμμα βλέπει κανείς ότι :
Vn→0 καθώς n→∞
Μπορείτε να δείξετε, ότι ο όγκος τείνει στο μηδέν καθώς το n τείνει στο άπειρο, χωρίς να χρησιμοποιήσετε ή να γράψετε μαθηματικούς τύπους;
Απαντήσεις ΕΔΩ: kolount.wordpress.com
Κατηγορίες:ΜΑΘΗΜΑΤΙΚΑ
Δεν είμαι σίγουρος τι εννοείς χωρίς μαθηματικούς τύπους, αλλά να μια σκέψη.
Ο όγκος μιας υπερσφαίρας με διάσταση ν-1 σε έναν χώρο διάστασης ν είναι μέτρου μηδέν. Αν πας το ν στο άπειρο, το ν με το ν-1 έχουν την ίδια «δύναμη» και άρα δεν μπορείς να ξεχωρίσεις μία υπερσφαίρα με διάσταση ν από μία με διάσταση ν-1, άρα ο μόνος συνεπής τρόπος για να συμβιβάσεις τους όγκους τους είναι να είναι και οι δύο μηδενικοί.
Σε νιοστές διαστάσεις ο «όγκος» της σφαίρας, δηλ. η «ύπαρξη» των φαινόμενων ιδιοτήτων της μηδενίζεται λόγω στρέβλωσης των διαστάσεων σε όλο και πιο μικρό «όγκο». Ακριβώς το ίδιο συμβαίνει με τις υπερχορδές που λόγω «πολλών» διαστάσεων έχουν σχεδόν μηδενικό «όγκο»