Αρχική › ΒΑΡΥΤΗΤΑ › Το σύμπαν σε τέσσερα γράμματα

Το σύμπαν σε τέσσερα γράμματα

By on • ( 1 )

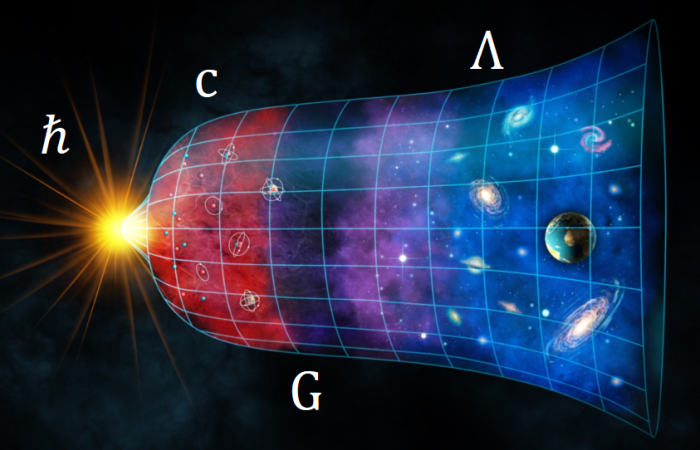
Το σύμπαν μέσα από τέσσερις σημαντικές φυσικές σταθερές (ταχύτητα φωτός c, σταθερά Planck ℏ, σταθερά παγκόσμιας έλξης G και κοσμολογική σταθερά Λ), των οποίων η παρουσία ή η απουσία διαμορφώνει ιδεατά την υφή της πραγματικότητας(*). 
Αυτοί οι σιωπηλοί αρχιτέκτονες γράφουν την ιστορία των πάντων, από την κβαντική βαρύτητα της κλίμακας Planck μέχρι το διαστελλόμενο σύμπαν de Sitter, από την μάζα του παρατηρήσιμου σύμπαντος μέχρι την μάζα του πρωτονίου. Ως αόρατοι ρυθμιστές καθορίζουν μήκη, χρόνους, μάζες και τον τρόπο που η φύση λειτουργεί σε διάφορες κλίμακες. Αναδεικνύουν μια όμορφη και κρυφή ενότητα στην δομή του κόσμου μας.

Το σύμπαν χωρίς το Λ

Αν θεωρήσουμε Λ=0 και συνδυάσουμε τις τρεις σταθερές που απομένουν c, ℏ και G, προκύπτει η διασημότερη κλίμακα: το μήκος Planck \ell_{P} = \sqrt{\dfrac{G \hbar}{c^{3}}} \approx 1,6 \cdot 10^{-35} \, m , ο χρόνος Planck t_{P} = \sqrt{\dfrac{G \hbar}{c^{5}}} \approx 5,4 \cdot 10^{-44} \, sec και η μάζα Planck: m_{P} = \sqrt{\dfrac{\hbar c}{G}} \approx 1,18 \cdot 10^{-8} \, kg.
Aυτές οι μονάδες έχουν ένα εξαιρετικό νόημα: ισούνται με το μέγεθος, τον χρόνο ημιζωής και την μάζα της μικρότερης δυνατής μαύρης τρύπας. Στο μήκος Planck \ell_{P} οι ιδέες του «εδώ» και «εκεί» διαλύονται – η κβαντομηχανική, η σχετικότητα και η βαρύτητα γίνονται αχώριστες. Το μήκος κύματος Compton ενός σωματιδίου με την μάζα Planck mP, λC=ℏ/(mP c), ισούται με την ακτίνα Schwarzschild, RS=2Gm/c2. Αυτό είναι το πεδίο του πολύ αρχέγονου σύμπαντος και της θερμοδυναμικής των μαύρων τρυπών, όπου ο Hawking έδειξε ότι οι μαύρες τρύπες μπορούσαν να ακτινοβολούν.

Το σύμπαν χωρίς το G

Αν μηδενίσουμε την σταθερά G του Νεύτωνα, από τις σταθερές ℏ, c και Λ προκύπτει ένας παράξενος κόσμος. Ένας κόσμος χωρίς βαρύτητα όπου οι μάζες δεν έλκονται μεταξύ τους. Όμως το Λ παραμένει δίνοντας στον κενό χώρο μια σταθερή καμπυλότητα. Οι φυσικές κλίμακες (μήκος και χρόνος) αυτού του σύμπαντος καθορίζονται από το Λ: \ell_{dS}=\Lambda^{-1/2} \approx 10^{26}m και t_{dS}=c^{-1} \Lambda^{-1/2} \approx 10^{17}sec = 10 \, Gyr Αυτές οι τιμές αντιστοιχούν προσεγγιστικά στην ακτίνα Hubble και την ηλικία του πραγματικού παρατηρήσιμου σύμπαντός μας. Αλλά η πιο εντυπωσιακή μονάδα είναι η μάζα: m_{dS}= \dfrac{\hbar}{c}\Lambda^{1/2} \approx 4 \cdot 10^{-69} kg. Σχεδόν μηδενική, αντιστοιχεί σε μήκος κύματος Compton που ισούται με την ακτίνα του ορίζοντα de Sitter \ell_{dS} και στην μάζα του ελαφρύτερου κβαντικού σωματιδίου που μπορεί να χωρέσει μέσα σε αυτό το σύμπαν.

Το σύμπαν χωρίς το ℏ

Αν θεωρήσουμε ένα σύμπαν όπου η κβαντική σταθερά ℏ ισούται με μηδέν, διατηρώντας τα Λ, c και G, τότε προκύπτει ένας κόσμος που αγνοεί τα κβαντικά φαινόμεναχ. Ο κόσμος της καθαρά κλασικής κοσμολογίας. Οι μονάδες μήκους και χρόνου εξακολουθούν να εκφράζονται από το Λ: \ell_{o}=\Lambda^{-1/2} και t_{o}=c^{-1} \Lambda^{-1/2}, αλλά η μάζα αλλάζει γιατί το G επέστρεψε: m_{0}= \dfrac{c^{2}}{G} \Lambda^{-1/2}. Μπορείτε να μαντέψετε την τιμή της; Ισούται περίπου με 1053 kg. Αυτή η τιμή είναι η εκτιμώμενη συνολική μάζα του παρατηρήσιμου σύμπαν! Δεν είναι σύμπτωση. Τα Λ και G δίνουν μια κρίσιμη πυκνότητα \rho_{c} = \Lambda c^{2} / (8 \pi G). Η μάζα μέσα σε μια σφαίρα ακτίνας Λ−1/2 είναι τάξης του mo. Έτσι, σε αυτό το κλασικό όριο, το Λ ορίζει την κλίμακα για όλα τα πράγματα στο σύμπαν.
Υπάρχει και κάτι ακόμα. Η κλίμακα επιτάχυνσης αο στην Τροποποιημένη Νευτώνεια Δυναμική του Milgrom (MOND), που προτάθηκε για να εξηγήσει την περιστροφή των γαλαξιών χωρίς αναφορά στην σκοτεινή ύλη, προσεγγίζεται πολύ καλά από την σχέση αο=c2√Λ. Ίσως το όριο της Νευτώνειας δυναμικής να είναι μια αντανάκλαση της συνολικής γεωμετρίας του σύμπαντος, η οποία κυριαρχείται από την κοσμολογική σταθερά Λ.

O αδρονικός ψίθυρος (c \rightarrow \infty )

Σε ένα μη σχετικιστικό σύμπαν η ταχύτητα του φωτός c θεωρείται άπειρη. Εδώ, το μήκος και ο χρόνος εξακολουθούν να καθορίζονται από το Λ, αλλά η κλίμακα της μάζας γίνεται: m_{nr} \sim \left( \dfrac{ \hbar^{2} \sqrt{\Lambda}}{G} \right) . Από την σχέση αυτή προκύπτει μια μάζα περίπου 10-27 kg, που αντιστοιχεί στην μάζα των πρωτονίων. Ο Weinberg το ανέφερε αυτό ως μια περίεργη διαστατική σύμπτωση. Αλλά εδώ, αναδύεται ως η κλίμακα μάζας για έναν μη σχετικιστικό κβαντικό κόσμο, σε έναν Λ-κόσμο. Πρόκειται για έναν υπαινιγμό ότι το Λ, η σταθερά του μακρόκοσμου, μπορεί να συνδέεται με την μάζα των δομικών στοιχείων της ύλης.

Ένας φορτισμένος επίλογος

Το 1881 G. J. Stoney, προσπαθώντας να ενοποιήσει την βαρύτητα με τον ηλεκτρομαγνητισμό, χρησιμοποίησε τις σταθερές G, c και e (=10−19 C, το στοιχειώδες ηλεκτρικό φορτίο), ορίζοντας τις μονάδες Stoney: \ell_{S}= \sqrt{\dfrac{G \, e^{2}}{4 \pi \epsilon_{0} c^{4}}}, m_{S}=\sqrt{\dfrac{e^{2}}{4 \pi \epsilon_{0}G}} και t_{S}= \sqrt{\dfrac{G \, e^{2}}{4 \pi \epsilon_{0} c^{6}}}. Οι μονάδες Stoney περιγράφουν έναν κόσμο στον οποίο υπάρχει βαρύτητα και ηλεκτρομαγνητισμός, αλλά αγνοούν πλήρως την κβαντική φύση της ύλης. Μας δείχνουν πού συναντώνται ο ηλεκτρομαγνητισμός και η βαρύτητα. O Planck αργότερα συμπεριέλαβε στις μονάδες Stoney την σταθερά ℏ, συνδέοντάς τες με τις μονάδες Planck διαμέσου της σταθεράς λεπτής υφής α=e2/(4πε0ℏc)≈1/137: (μονάδες Stoney)≈(μονάδες Planck)/137.

διαβάστε περισσότερες λεπτομέρειες: Pedro Bargueño, The Universe in four letters: a bedtime history –https://arxiv.org/abs/2512.21355

(*)
Η ταχύτητα του φωτός c≈300.000 km/sec είναι η μέγιστη ταχύτητα οποιουδήποτε αντικειμένου στο σύμπαν έχει πρωταγωνιστικό ρόλο στην θεωρία της σχετικότητας του Αϊνστάιν.
Η σταθερά του Πλανκ \hbar=h/2π, με h≈6,6·10-34 J·s. εμφανίζεται στην κβαντική θεωρία που περιγράφει τον μικρόκοσμο, π.χ. στην αρχή της αβεβαιότητας.
Η σταθερά της βαρύτητας G≈6,7·10-11 N·m2/kg2, εμφανίζεται στο νόμο της παγκόσμιας έλξης του Νεύτωνα, σύμφωνα με τον οποίο δύο μάζες έλκονται αμοιβαίως με δύναμη ανάλογη τόσο του γινομένου μαζών τους όσο και της βαρυτικής σταθεράς G και αντιστρόφως ανάλογη με το τετράγωνο της απόστασής τους.
Η κοσμολογική σταθερά Λ εισήχθη από τον Αϊνστάιν ως μια τροποποίηση στην γενική σχετικότητα ώστε να επιτύχει ένα στατικό σύμπαν, κατέληξε σήμερα να εκφράζει την σκοτεινή ενέργεια, στην οποία αποδίδεται η επιταχυνόμενη διαστολή του σύμπαντος.

‹
›

Κατηγορίες:ΒΑΡΥΤΗΤΑ, ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ, ΚΒΑΝΤΙΚΗ ΘΕΩΡΙΑ, ΚΟΣΜΟΛΟΓΙΑ, ΜΑΥΡΕΣ ΤΡΥΠΕΣ, ΣΤΟΙΧΕΙΩΔΗ ΣΩΜΑΤΙΑ, ΣΥΜΠΑΝ, ΣΧΕΤΙΚΟΤΗΤΑ, ΦΥΣΙΚΗ

Ετικέτες:

1 reply

  1. Αθανασία's avatar
    Αθανασία
    05/01/2026 • 2:00 μμ

    Είναι και το e. Μαθηματική σταθερά αλλά πιστεύω διαισθητικά, ότι κι αυτή παίζει τον ρόλο της.

    Reply ↓

Σχολιάστε

Ο ιστότοπος χρησιμοποιεί το Akismet για την εξάλειψη των ανεπιθύμητων σχολίων. Μάθετε πως επεξεργάζονται τα δεδομένα των σχολίων σας.