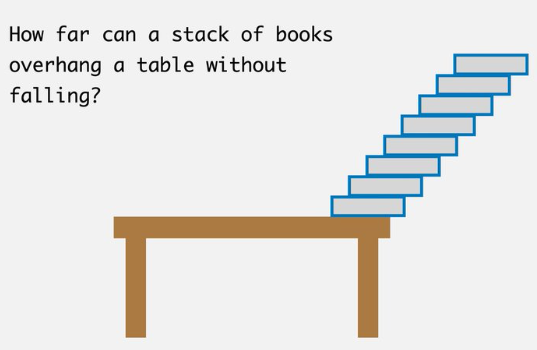
Πάρτε μια οποιαδήποτε κανονική τράπουλα με 52 χαρτιά, και βάλτε την στο τραπέζι. Με το δάκτυλό σας μετακινείστε το πάνω χαρτί, χωρίς να μετακινήσετε κανένα άλλο. Πόσο μακριά μπορείτε να το μετακινήσετε πριν πέσει; Ή, για να το πούμε διαφορετικά πόσο μπορεί να εξέχει το πάνω χαρτί από την υπόλοιπη στοίβα;
Η απάντηση είναι απλή: μπορεί να εξέχει κατά το μισό του μήκος, όπως φαίνεται στο παραπάνω σχήμα 1. Αν το σπρώξετε έτσι ώστε να εξέχει περισσότερο από το μισό του μήκος, το χαρτί θα πέσει. Το κρίσιμο σημείο είναι το κέντρο βάρους του χαρτιού, που βρίσκεται στο μέσο του.
Ας προχωρήσουμε τώρα λίγο περισσότερο. Με το πάνω χαρτί να εξέχει κατά ο μισό του μήκος – δηλαδή, όσο πιο πολύ γίνεται – σπρώξτε με το δάκτυλό σας το δεύτερο χαρτί. Πόσο μπορεί να εξέχει ο συνδυασμός αυτών των δύο πάνω χαρτιών;
Για να το βρείτε φανταστείτε αυτά τα δυο χαρτιά ως ένα ενιαίο σώμα. Πού βρίσκεται το κέντρο βάρους αυτού του σώματος; Βρίσκεται, όπως και πριν, στο μέσο του. Καθώς το συνολικό μήκος είναι ίσο με ενάμισι χαρτί της τράπουλα, το μέσο βρίσκεται στα τρία τέταρτα του πάνω χαρτιού (σχήμα 2).
Συνεπώς, το ενιαίο σώμα των δυο πάνω χαρτιών εξέχει κατά τα τρία τέταρτα του ενός χαρτιού.
Αν τώρα αρχίσετε να σπρώχνετε το τρίτο χαρτί για να για να διαπιστώσετε πόσο μπορείτε να αυξήσετε την προεξοχή, θα διαπιστώσετε ότι μπορείτε να το σπρώξετε μόνο κατά το ένα έκτο του μήκους του. Πάλι το κόλπο είναι να θεωρήσετε τα τρία πάνω χαρτιά ως ένα ενιάιο σώμα. Το κέντρο βάρους βρίσκεται στο ένα έκτο του μήκους του τρίτου χαρτιού (σχήμα 3).
Μπροστά από αυτό το σημείο βρίσκεται το ένα έκτο του τρίτου χαρτιού, το ένα έκτο συν το ένα τέταρτο του δεύτερου χαρτιού και το ένα έκτο συν το ένα δεύτερο του πρώτου χαρτιού. Το συνολικό άθροισμα είναι ενάμισι χαρτί:
To μισό δηλαδή των τριών χαρτιών βρίσκεται μπορστά, και το άλλο μισό πίσω από το κρίσιμο. Αυτό θα συμβεί αφού σπρώξουμε το τρίτο χαρτί ώστε να εξέχει όσο το δυνατόν περισσότερο (σχήμα 4).
Έτσι, το συνολικό μήκος που εξέχει το σύστημα των τριών χαρτιών είναι ένα δεύτερο (από το πρώτο χαρτί) συν ένα τέταρτο (από το δεύτερο χαρτί) συν ένα έκτο από το τρίτο χαρτί). Αυτό μας δίνει το εντυπωσιακό σύνολο των ένδεκα δωδεκάτων του χαρτιού!
Μπορεί ένας συνδυασμός περισσότερων χαρτιών να εξέχει πάνω από το μήκος ενός χαρτιού; Η απάντηση είναι ναι. Το αμέσως επόμενο χαρτί – το τέταρτο – αν το σπρώξουμε προσεκτικά, συνεισφέρει ακόμα ένα όγδοο στο συνολικό μήκος. Δεν πρόκειται κάνω τις πράξεις. Ο αναγνώστης ή θα με πιστέψει ή θα κάνει τις πράξεις μόνος του, όπως τις έκανα εγώ τα για τα τρία πρώτα χαρτιά. Το συνολικό μήκος με τέσσερα χαρτιά θα είναι: ένα δεύτερο συν ένα τέταρτο συν ένα έκτο συν ένα όγδοο – συνολικά δηλαδή, ένα συν ένα εικοστό τέταρτο του ενός χαρτιού (σχήμα 5).
Αν συνεχίσουμε σπρώχνοντας μέχρι και το 51ο χαρτί (δεν έχει νόημα να σπρώξουμε το 52ο) θα φτάσουμε σ’ ένα συνολικό μήκος:
Aυτό ισούται περίπου με 2,25940659073334. Μπορούμε, δηλαδή, να πετύχουμε μια συνολική προεξοχή μεγαλύτερη από δυο χαρτιά και ένα τέταρτο! (σχήμα 6)
Αυτά τα έμαθα όταν ήμουν προπτυχιακός φοιτητής. Στη διάρκεια των καλοκαιρινών διακοπών μου, προσπαθούσα να προετοιμαστώ για το επόμενο εξάμηνο με στόχο να βελτιώσω την επίδοσή μου. Για να συμβάλλω στην χρηματοδότηση των σπουδών μου, συνήθιζα, κατά τις καλοκαιρινές διακοπές, να εργάζομαι σε διάφορες οικοδομές. Εκείνη την εποχή στην Αγγλία, η συγκεκριμένη εργασία δεν ελεγχόταν από τα συνδικάτα. Την επομένη της ημέρας που ανακάλυψα αυτή την ιστορία με τα χαρτιά της τράπουλας, έμεινα μόνος σ’ έναν κλειστό χώρο γεμάτο ωραίες τετράγωνες τάβλες, με εντολή αν τις συμμαζέψω. Πέρασα δυο ευτυχισμένες ώρες με 52 από δαύτες, προσπαθώντας να δημιουρήσω μια προεξοχή μήκους δυο κι ένα τέταρτο της τάβλας. Όταν ήρθε ο επιστάτης και με βρήκε σε βαθιά περίσκεψη μπροστά σ’ έναν κρεμαστό πύργο από τάβλες, υποθέτω πως οι κάποιοι ενδοιασμοί του σχετικά με την πρόσληψη φοιτητών στην οικοδομή δικαιώθηκαν.
Tίθεται λοιπόν εύλογα το ερώτημα: Αν διαθέταμε απεριόριστο αριθμό τραπουλοχάρτων, υπάρχει κάποιο μέγιστο μήκος προέκτασης που δεν μπορούμε να ξεπεράσουμε; Πέρα από κάθε διαίσθηση η απάντηση είναι πως δεν υπάρχει! Πράγματι, αν εφαρμόσουμε τα παραπάνω σε «άπειρα» τραπουλόχαρτα προκύπτει το άθροισμα απείρων όρων: . Βγάζοντας κοινό παράγοντα το 1/2 προκύπτει στην παρένθεση η αρμονική σειρά:
, η οποία αποκλίνει(*).
πηγή: John Derbyshire «Υπόθεση Ρίμαν – Η εμμονή με τους πρώτους αριθμούς» , εκδόσεις Τραυλός – https://nap.nationalacademies.org/read/10532/chapter/3#17 – https://x.com/fermatslibrary/status/1893407441007624314
(*) Μια γρήγορη απόδειξη: το άθροισμα (1/3+1/4) είναι μεγαλύτερο από το 1/2. Το ίδιο ισχύει για το (1/5+1/6+1/7+1/8), το ίδιο και για το (1/9+1/10+1/11+1/12+1/13+1/14+1/15+1/16) κ.ο.κ. Με άλλα λόγια, παίρνοντας 2 όρους, ύστερα 4, ύστερα 8, ύστερα 16 και ούτω καθεξής, μπορούμε να ομαδοποιήσουμε τη σειρά σε άπειρα μπλοκ, άπειρα επί μέρους αθροίσματα που όλα είναι μεγαλύτερα από το ένα δεύτερο. Συνεπώς, το συνολικό άθροισμα πρέπει να είναι άπειρο. Αυτή η απόδειξη έγινε από τον Nicole Oresme τον 14ο αιώνα.
Κατηγορίες:ΜΑΘΗΜΑΤΙΚΑ, ΜΗΧΑΝΙΚΗ






Σχολιάστε