Ο Αϊνστάιν με την δημοσίευση της ειδικής θεωρίας της σχετικότητας το 1905, επισήμανε ότι το ταυτόχρονο δυο γεγονότων τα οποία συντελούνται σε διαφορετικές θέσεις δεν αποτελεί μία απόλυτη και άνευ όρων σχέση μεταξύ των γεγονότων: είναι περισσότερο ένας τρόπος να μιλήσουμε για αυτά τα γεγονότα, κατάλληλος για ένα συγκεκριμένο σύστημα αναφοράς, αλλά ακατάλληλος για τα συστήματα αναφοράς που κινούνται σε σχέση με το συγκεκριμένο σύστημα αναφοράς κατά μήκος της γραμμής που ενώνει τα γεγονότα.
Αυτό ήταν ήδη γνωστό και πριν το 1905 και αφορούσε τη χωρική σχέση ανάμεσα σε δυο γεγονότα που συντελούνται σε διαφορετικές στιγμές στον χρόνο (αν συντελούνται ή όχι στην ίδια θέση στον χώρο, προφανώς εξαρτάται από το σύστημα αναφοράς). Ακριβώς το ίδιο ισχύει και για τις χρονικές στιγμές ανάμεσα σε δυο γεγονότα, όμως οι επιστήμονες που είχαν αρχίσει να ερευνούν το θέμα του χρόνου και πριν από το 1905 δεν ήταν σε θέση να το αντιληφθούν. Και αυτό διότι στην ανθρώπινη κλίμακα χρόνων και αποστάσεων, ο χρόνος που αντιστοιχεί σε μία δεδομένη απόσταση είναι μόνο 1 νανοδευτερόλεπτο ανά πόδι, δηλαδή πολύ μικρός για να παρατηρηθεί.
Η διορατικότητα του Αϊνστάιν σχετικά με τη συμβατική φύση του ταυτοχρονισμού υπονοεί ότι ο ρυθμός ενός ρολογιού και το μήκος μιας ράβδου εξαρτώνται από το σύστημα αναφοράς στο οποίο τα μετράμε. Στην περίπτωση της ράβδου, η εξάρτηση από το σύστημα αναφοράς αποτελεί μία στοιχειώδη συνέπεια του γεγονότος ότι για να μετρήσουμε το μήκος μιας κινούμενης ράβδου πρέπει να παρατηρήσουμε που βρίσκονται οι δυο άκρες της ράβδου ακριβώς την ίδια χρονική στιγμή, έτσι ώστε αν η «ίδια χρονική στιγμή» ποικίλλει από το ένα σύστημα αναφοράς στο άλλο, τότε ποικίλλει ανάλογα με το μήκος της ράβδου. Στην περίπτωση του ρολογιού, για να μετρήσουμε τον ρυθμό του πρέπει να παρατηρήσουμε τις ενδείξεις του ρολογιού σε δυο διαφορετικές χρονικές στιγμές, έτσι ώστε αν το ρολόι κινείται θα πρέπει να το συγκρίνουμε με συγχρονισμένα και ακίνητα ρολόγια που βρίσκονται σε διαφορετικές θέσεις. Όμως, αν το ταυτόχρονο των γεγονότων που συντελούνται σε δυο διαφορετικές θέσεις είναι άμεσα εξαρτώμενο από το σύστημα αναφοράς, τότε και ο συγχρονισμός των ρολογιών σε δύο διαφορετικές θέσεις θα είναι άμεσα εξαρτώμενος από το σύστημα αναφοράς. Επομένως, οι όποιες διαφωνίες σχετικά με τον ταυτοχρονισμό όταν μεταφερόμαστε από ένα σύστημα αναφοράς σε ένα άλλο, ανάγονται υποχρεωτικά και σε διαφωνίες σχετικά με τον ρυθμό των κινούμενων ρολογιών και το μήκος των κινούμενων ράβδων.
Τώρα, όμως, θα αναρωτηθείτε τι είναι αυτό που κάνει τις κινούμενες ράβδους να συστέλλονται και τι είναι αυτό που κάνει τα κινούμενα ρολόγια να επιβραδύνονται; Οι αλλαγές αυτές συμβαίνουν στην πραγματικότητα; Ή είναι απλώς δευτερεύουσες εκφάνσεις των διαφωνιών σχετικά με το ταυτόχρονο δύο γεγονότων οι οποίες οδηγούν με τη σειρά τους σε διαφωνίες σχετικά με τις προϋποθέσεις που ορίζουν μια μέτρηση ως έγκυρη; Αυτό που μπορούμε να πούμε με σιγουριά είναι ότι δεν επικρατεί ομοφωνία ανάμεσα στους εν ενεργεία φυσικούς σχετικά με τη σωστή απάντηση στις παραπάνω ερωτήσεις. Πολλές φορές ερχόμαστε αντιμέτωποι με τους ισχυρισμούς κάποιων φυσικών που υποστηρίζουν, για παράδειγμα, ότι τα κινούμενα ρολόγια φαίνεται ότι επιβραδύνονται όταν ο ρυθμός τους μετριέται από ακίνητα ρολόγια, ή ότι οι κινούμενες ράβδοι φαίνεται ότι συστέλλονται.
Αυτή όμως η επιφυλακτική τοποθέτηση είναι τελείως αδικαιολόγητη. Τα κινούμενα ρολόγια όντως συστέλλονται, αν η έννοια του ρυθμού ενός ρολογιού ή του μήκους μιας ράβδου έχουν εξαρχής κάπoιο νόημα. Τα ρολόγια και οι ράβδοι πρέπει να συμπεριφέρονται με αυτόν τον τρόπο, καθώς η συμπεριφορά τους απορρέει κατευθείαν από τους κανόνες για ταυτόχρονα γεγονότα και για συγχρονισμένα ρολόγια. Τα ρολόγια και οι ράβδοι οφείλουν να έχουν αυτή τη συμπεριφορά, αν θέλουμε το όλο θέμα που εξετάζουμε να έχει απόλυτη συνοχή και να μην καταρρεύσει λόγω της δικής του ανακολουθίας.
Αλλά αυτή η απάντηση δεν είναι καθόλου ικανοποιητική. Θα επιθυμούσαμε να υπάρχει κάποιος μηχανισμός. Τι είναι αυτό που προκαλεί τα ρολόγια να επιβραδύνονται; Τι είναι αυτό που προκαλεί τις κινούμενες ράβδους να συστέλλονται; Αν η μόνη διαθέσιμη εξήγηση είναι ότι τα κινούμενα ρολόγια επιβραδύνονται και οι κινούμενες ράβδοι συστέλλονται για να διατηρήσουν τη συνοχή της σχετικότητας, θα μπορούσε κανείς να αναρωτηθεί γιατί τα ρολόγια και οι ράβδοι ενδιαφέρονται τόσο για τη σχετικότητα. Αυτό που πραγματικά χρειαζόμαστε είναι μια εξήγηση η οποία να βασίζεται σε αυτό το δομικό στοιχείο της κατασκευής ράβδων το οποίο αναγκάζει τις ράβδους να συσταλούν κατά μήκος της διεύθυνσης της κίνησής τους, όπως και στο αντίστοιχο δομικό στοιχείο του μηχανισμού των ρολογιών το οποίο αναγκάζει τα ρολόγια να επιβραδύνουν όταν βρίσκονται σε κίνηση, έτσι ώστε και η συστολή και η επιβράδυνση να υπολογίζονται από τον συντελεστή .
Kαι πράγματι μπορούμε να προσδιορίσουμε τέτοιους μηχανισμούς, αν και συχνά αποδεικνύεται αρκετά περίπλοκο ως διαδικασία. Μέσα σε ένα οποιοδήποτε σύστημα αναφοράς, οι νόμοι της φυσικής που διέπουν το μήκος των ράβδων και τον ρυθμό των ρολογιών παρέχουν ολοκληρωμένες και πειστικές εξηγήσεις γιατί μια ράβδος πρέπει να συστέλλεται όταν τη θέτουμε σε κίνηση ως προς τη διεύθυνση του μήκους, και γιατί ο ρυθμός ενός ρολογιού πρέπει να ελαττώνεται όταν το ρολόι αρχίζει να κινείται. Οι άνθρωποι που στογγυλεύουν τα λόγια τους χρησιμοποιώνας τη φράση «φαίνεται ότι» δεν έχουν κατανοήσει ακριβώς τι συμβαίνει.
Ας σκεφτούμε, για παράδειγμα, ένα κανονικό ρολόι το οποίο τρέχει αργά όταν κινείται, για έναν πολύ απλό λόγο. Πάρτε μια ακίνητη ράβδο μήκους D, τοποθετήστε δυο καθρέφτες σε κάθε άκρη της ράβδου που να αντανακλούν το φως προς τα πίσω κατά μήκος της ράβδου και αφήστε έναν παλμό φωτός να αναπηδήσει μπρος πίσω κατά μήκος της ράβδου από τον έναν καθρέφτη στον άλλο.
Το ρολόι χτυπά κάθε φορά που ο παλμός ολοκληρώνει μια διαδρομή – από τον έναν καθρέφτη στον άλλο. Αν και είναι δύσκολο να κατασκευάσουμε ένα ρολόι το οποίο να λειτουργεί με αυτόν τον τρόπο, το συγκεκριμένο ρολόι έχει έχει το προτέρημα της ενοιολογικής απλότητας. Ακριβώς για αυτό, χρειάζεται να γνωρίζουμε μόνο δυο στοιχεία για τη λειτουργία του φυσικού κόσμου έτσι ώστε να αναλύσουμε πώς συμπεριφέρεται το ρολόι όταν κινείται: πόσο γρήγορα τρέχει το φως στο κινούμενο ρολόι και πόσο είναι το μήκος της ράβδου όταν αυτή κινείται. Γνωρίζουμε ότι η ταχύτητα του φωτός παραμένει ίση με c σε οποιοδήποτε ανδρανειακό σύστημα αναφοράς, επομένως απαντάμε στο πρώτο ζητούμενο.Τώρα, όμως, μπορεί να ανησυχήσετε ότι θα πρέπει να ασχοληθούμε με τον μηχανισμό που προκαλεί τη συστολή των κινούμενων ράβδων για να κατανοήσουμε το μήκος του κινούμενου ρολογιού. Ευτυχώς, υπάρχει ένας εύκολος τρόπος για να αποφύγουμε αυτό το πρόβλημα: απαιτούμε η ράβδος να μην κινείται παράλληλα με τον εαυτό της παρά μόνο στην κάθετη διεύθυνση, όπως φαίνεται στο σχήμα.
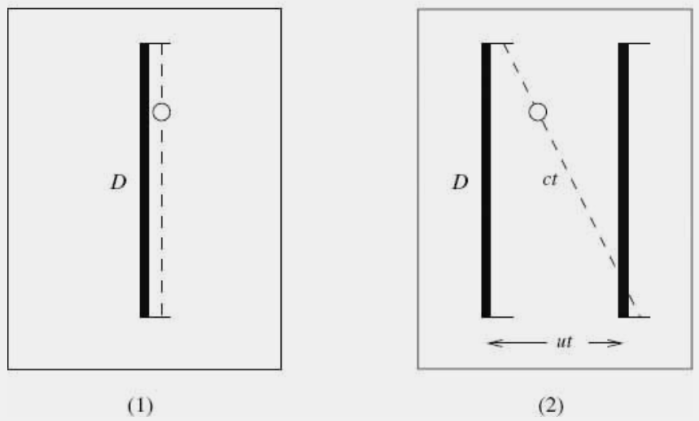
Μια ράβδος η οποία κινείται κάθετα στο μήκος της δεν συστέλλεται – ούτε διαστέλλεται. Αυτό συμβαίνει, γιατί, σε αντίθεση με τα συστήματα αναφοράς τα οποία κινούνται κατά μήκος της γραμμής που ενώνει δυο γεγονότα, δεν υπάρχει τίποτα το προβληματικό σχετικά με το ταυτόχρονο των γεγονότων που συντελούνται σε δυο διαφορετικές θέσεις στον χώρο, όταν αναφερόμαστε σε συστήματα αναφοράς τα οποία κινούνται κάθετα στη γραμμή που ενώνει τα δύο γεγονότα.
Όταν το ρολόι είναι ακίνητο, ο χρόνος που απαιτείται για να φτάσει από τη μιά άκρη της ράβδου στην άλλη είναι ίσος με D/c, έτσι ώστε ο χρόνος Τ που απαιτείται ανάμεσα στους χτύπους του ρολογιού να είναι: (1).
Ωστόσο, όταν το ρολόι κινείται (βλέπε παραπάνω σχήμα) το φως πρέπει να καλύψει μεγαλύτερη απόσταση για να φτάσει από τη μία άκρη της ράβδου στην άλλη – και επειδή η ταχύτητα του φωτός είναι ανεξάρτητη από οποιδήποτε σύστημα αναφοράς, προφανώς μεσολαβεί περισσότερος χρόνος ανάμεσα στους χτύπους του ρολογιού. Ο μηχανισμός είναι τόσο απλός.
Πράγματι μπορούμε να εξάγουμε μία ποσοτική έκφραση για αυτόν τον επιπρόσθετο χρόνο. Αν η ταχύτητα της ράβδου είναι v και ο χρόνος που χρειάζεται το φως για να κινηθεί από τη μια άκρη της ράβδου στην άλλη είναι t, τότε η ράβδος καλύπτει απόσταση vt, κάθετη στο μήκος της ράβδου, μεταξύ της αναχώρησης του φωτός από τη μία άκρη της άφιξής του στην άλλη άκρη. Eπομένως, η απόσταση που πρέπει να διανύσει το φως είναι η υποτείνουσα ενός ορθογωνίου τριγώνου, όπου η μία πλευρά του είναι ίση με το μήκος D της ράβδου – το οποίο δεν μεταβάλλεται – και η άλλη πλευρά του είναι ίση με vt. Eφόσον αυτή η απόσταση αντιστοιχεί στην απόσταση ct που καλύπτει το φως σε χρόνο t, από το Πυθαγόρειο θεώρημα παίρνουμε ότι: και επομένως
Eπειδή ο χρόνος που μεσολαβεί μεταξύ των δύο χτύπων του κινούμενου ρολογιού θα έχουμε χρησιμοποιώντας την εξ. (1) ότι
Στο κινούμενο ρολόι μεσολαβεί περισσότερος χρόνος μεταξύ των χτύπων του συγκριτικά με το ακίνητο ρολόι.
Θα μπορούσε κανείς να αντιμετωπίσει με καχυποψία το συγκεκριμένο παράδειγμα λέγοντας ότι δεν επιλέχθηκε για την απλότητά του, αλλά για να εκμεταλλευτεί τη σταθερότητα της ταχύτητας του φωτός η οποία μπορεί να μας δώσει τον ζητούμενο «μηχανισμό» σχετικά με την επιβράδυνση των ρολογιών. Μια τέτοια καχύποπτη αντίδραση δεν είναι λογική όμως. Η αρχή της σταθερότητας της ταχύτητας του φωτός αποτελεί τόσο θεμελιώδες χαρακτηριστικό του κόσμου στον οποίο ζούμε, όσο θεμελιώδης είναι και οποιαδήποτε άλλη φυσική ιδιότητα. Κάποιοι ίσως να πουν ότι η σταθερότητα της ταχύτητας του φωτός αποτελεί στην πραγματικότητα το πιο θεμελιώδες φυσικό χαρακτηριστικό. Επομένως, είναι απόλυτα παρωχημένη – τουλάχιστον κατά έναν αιώνα – και εντελώς παράλογη η αντίληψη να επιμένει κανείς ότι δεν θα εκμεταλλευτούμε την αρχή προς όφελός μας για τον σχεδιασμό εργαλείων και την ανακάλυψη μηχανισμών.
Επιπλέον, πάντα μπορούμε να βρούμε έναν μηχανισμό, όποια κι αν είναι η κατασκευή του ρολογιού. Μόνο που αποδεικνύεται πιο περίπλοκο για τα περισσότερα ρολόγια. Η λειτουργία ενός μοντέρνου ατομκού ρολογιού, για παράδειγμα, βασίζεται στη συχνότητα της δόνησης ενός συγκεκριμένου ατόμου, κάτω από συγκεκριμένες συνθήκες. Τέτοιοι ρυθμοί δονήσεων διέπονται από περίπλοκες εξισώσεις της κβαντομηχανικής, οι οποίες διατυπώθηκαν για πρώτη φορά από τον Paul Dirac. Και πράγματι, αν χρησιμοποιήσετε την εξίσωση του Dirac για να υπολογίσετε τη συχνότητα δόνησης του συγκεκριμένου ατόμου, κάτω από συγκεκριμένες συνθήκες, ενώ θεωρήσετε ότι ολόκληρο το ρολόι κινείται τώρα με ταχύτητα v, θα βρείτε – μετά από αρκετή προσπάθεια – ότι η κίνηση του ρολογιού μειώνει τον ρυθμό δόνησης του ατόμου κατά ακριβώς το συντελεστή επιβράδυνσης .
Ακόμα και ο ρυθμός ενός κλασικού μηχανικού ρολογιού διέπεται από την ελαστικότητα συγκεκριμένων χορδών ή από την αδράνεια συγκεκριμένων τροχών. Αυτά με τη σειρά τους καθορίζονται από τις δυνάμεις – σχεδόν ηλεκτρομαγνητικής φύσης – οι οποίες συγκρατούν ενωμένα τα άτομα που σχηματίζουν τις χορδές και τους τροχούς, αλλά αποκελιστικά ηλεκτρομαγνητικής φύσης – οι οποίες συγκρατούν ενωμένα τα άτομα που σχηματίζουν τις χορδές και τους τροχούς, αλλά και από τους νόμους της κβαντομηχανικής οι οποίοι καθορίζουν τη δομή των ατόμων υπό την παρουσία αυτών των δυνάμεων. Και παρόλο που κανένας, από όσο γνωρίζω, δεν έχει πραγματοποιήσει ποτέ έναν λεπτομερή υπολογισμό των «αρχικών συνθηκών» του ρυθμού ενός κινούμενου ρολογιού, ξεκινώντας από αυτό το θεμελιώδες επίπεδο, σας εγγυώμαι ότι η επίδραση της κίνησης στη δράση των δυνάμεων αυτών είναι ικανή να μειώσει τον αριθμό του ρολογιού κατά τον συντελεστή επιβράδυνσης.
Πως μπορώ να σας εγγυηθώ κάτι τέτοιο, χωρίς να χρειαστεί να καταφύγω σε έναν δύσκολο υπολογισμό; Θυμηθείτε το πρώτο αξίωμα του Αϊνστάιν. Οι νόμοι του ηλεκτρομαγνητισμού, όπως και οι νόμοι της μηχανικής, πρέπει να είναι συνεπείς με την αρχή της σχετικότητας. Ένα από τα επιτεύγματα του Αϊνστάιν στο άρθρο του το 1905 ήταν η λεπτομερής επίδειξη πώς αυτοί οι νόμοι θα μπορούσαν να διατυπωθούν σε μία μορφή η οποία να είναι απόλυτα συνεπής με την αρχή της σχετικότητας.
Με άλλα λόγια, οι νόμοι της κβαντομηχανικής – γνωστοί και ως «σχετικιστή κβαντομηχανική» – και του ηλεκτρομαγνητισμού, όπως τους γνωρίζουμε σήμερα, έχουν οριστεί σε αυτή τη μορφή, έτσι ώστε όταν εφαρμόζονται για να υπολογίσουμε τον ρυθμό ενός κινούμενου ρολογιού, το αποτέλεσμα που προκύπτει πρέπει να δείχνει ότι το κινούμενο ρολόι τρέχει αργά. Επίσης, έχουν οριστεί σε αυτή τη μορφή για να εξασφαλίζουν ότι οι δυνάμεις που συγκρατούν μία ράβδο συμπεριφέρονται με τέτοιον τρόπο, έτσι ώστε η ράβδος να συστέλλεται όταν τίθεται σε κίνηση. Αυτοί οι νόμοι πρέπει, όταν εφαρμόζονται σε αυτές τις καταστάσεις, να μας βοηθούν να κάνουμε μια λεπτομερή εκτίμηση – η οποία όμως μπορεί να μας δυσκολέψει αρκετά, απαιτώντας τεράστια υπολογιστική προσπάθεια – των φυσικών λόγων για τους οποίους τα κινούμενα ρολόγια επιβραδύνονται και οι κινούμενοι ράβδοι συστέλλονται.
Το γεγονός ότι οι νόμοι μιας θεωρίας έχουν αυτή τη μορφή, συχνά συνοψίζεται από τον ισχυρισμό ότι η εκάστοτε θεωρία αποτελεί ένα «αναλλοίωτο Lorentz» ή «συναλλοίωτο Lorentz». Η ορολογία αυτή δόθηκε προς τιμήν του H. A. Lorentz ο οποίος δημοσίευσε το 1904 τη συναλλοίωτη μορφή Lorentz για τους νόμους του ηλεκτρομαγνητισμού, χωρίς όμως να έχει κατανοήσει πλήρως τη σημασία αυτού του επιτεύγματος. Ο Αϊνστάιν ήταν αυτός που ενσωμάτωσε πρώτος τη μορφή Lorentz στη δημοσίευσή του το 1905 σχετικά με τη φύση του χρόνου.
Αυτή, όμως, η επιμονή μας, ότι κάθε έγκυρη θεωρία της φυσικής πρέπει να απαιτεί ότι τα κινούμενα ρολόγια επιβραδύνονται και οι κινούμενες ράβδοι συστέλλονται, μήπως πρόκειται τελικά για μία κολοσσιαία απάτη – ή ακόμα αυταπάτη; Μήπως έχουμε επινοήσει μηχανισμούς οι οποίοι εξηγούν αυτά τα φαινόμενα, μόνο και μόνο επειδή αρνούμαστε να δώσουμε βάση σε οποιαδήποτε άλλη θεμελιώδη θεωρία η οποία δεν περιλαμβάνει τους μηχανισμούς αυτούς;
Σκεφτείτε κάποιες άλλες, πιο εύληπτες, αναλλοίωτες αρχές. Επιμένουμε ότι οποιαδήποτε αποδεκτή θεμελιώδης θεωρία δεν κάνει καμία διάκριση η οποία να βασίζεται σε απόλυτο προσανατολισμό. Αυτές οι θεωρίες έχουν βασιστεί στην αρχή του αναλλοίωτου σε στροφές. Μας δίνουν τη δυνατότητα να εξηγήσουμε με τη βοήθεια ενός μηχανισμού γιατί μπορεί κάποιος να ρίξει μια μπάλα σε μακρινή απόσταση τόσο προς τα βορειοανατολικά όσο και προς βορειοδυτικά – ανεξάρτητα από τον άνεμο, την περιστροφή της Γης και άλλες τοπικές ασυνάφειες. Είναι απάτη; Όχι! Αν τυχόν ανακαλύπταμε ποτέ ότι υπάρχει πραγματικά μία ιδιαίτερη κατεύθυνση ενσωματωμένη στη δομή του κενού χώρου, η ανακάλυψη αυτή θα ερμηνευόταν ως αποτυχία ενός βασικού νόμου και θα είχε να μας διδάξει κάτι πολύ σημαντικό. Εφόσον, όμως, η αρχή του αναλλοίωτου σε στροφές είναι σωστή, – σύμφωνα με όσα γνωρίζουμε μέχρι σήμερα – θα ήταν ανόητο να μην την ενσωματώναμε στη θεμελιώδη διατύπωση της φυσικής θεωρίας.
Ακριβώς το ίδιο ισχύει και για την αρχή της σχετικότητας και για την αρχή της σταθερότητας της ταχύτητας του φωτός, η οποία περιγράφεται καλύτερα – σύμφωνα με αυτό το γενικό πλαίσιο – ως αρχή της ύπαρξης μίας αναλλοίωτης ταχύτητας, ή αν προτιμάτε, ως αρχή αναλλοίωτου του διαστήματος. Αυτές οι αρχές έχουν πλέον εδραιωθεί τόσο καλά ώστε στην προσπάθειά μας να διατυπώσουμε θεωρίες για την ερμηνεία νέων φαινομένων τα οποία δεν πλαισιώνονται, όμως, από τους νόμους του ηλεκτρομαγνητισμού, πρέπει να υιοθετήσουμε έναν κανόνα ο οποίος μας υποδεικνύει ότι αυτά τα νέα φαινόμενα πρέπει να είναι συνεπή με τις αρχές στις οποίες στηρίζεται η σχετικότητα. Για παράδειγμα, από το 1905 μέχρις ήμερα έχουμε ανακαλύψει δύο νέες δυνάμεις: τις ισχυρές αλληλεπιδράσεις οι οποίες συγκρατούν τους ατομικούς πυρήνες, παρά τις ηλεκτρικές απωθήσεις μεταξύ των πρωτονίων που σχηματίζουν τον πυρήνα, και τις ασθενείς αλληλεπιδράσεις οι οποίες διέπουν συγκεκριμένα είδη ραδιενεργών διασπάσεων, όπως τη διάσπαση ενός νετρονίου σε πρωτόνιο, σε ηλεκτρόνιο και σε νετρίνο.
Αυτές οι δυνάμεις δεν έχουν άμεση σχέση με τον ηλεκτρομαγνητισμό, παρόλο που οι ασθενείς και ηλεκτρομαγνητικές δυνάμεις συνδυάζονται πλέον σε μία «ηλεκτρασθενή» δύναμη η οποία εκδηλώνεται και στα δύο φαινόμενα. Στην προσπάθειά μας να βρούμε τους νόμους που διέπουν τις δυνάμεις αυτές, ερχόμαστε αντιμέτωποι με ισχυρούς περιορισμούς σύμφωνα με τις αρχές του αναλλοίωτου: οι νόμοι αυτοί πρέπει να είναι συνεπείς με την αρχή του αναλλοίωτου σε στροφές, την αρχή του αναλλοίωτου σε μεταθέσεις στον χρόνο και στον χώρο, με την αρχή της σχετικότητας και με την αρχή της σταθερότητας της αρχής του φωτός. Ως αποτέλεσμα, μπορούμε να εγγυηθούμε ότι αν σχεδιάσουμε οποιοδήποτε ρολόι το οποίο αξιοποιεί τις ισχυρές ή ασθενείς αλληλεπιδράσεις – όπως κάνει δηλαδή ένα ηλεκτρομαγνητικό ρολόι – το ρολόι αυτό θα τρέχει αργά κατά τέτοιον τρόπο ώστε ο ρυθμός του να δίνεται από τον συντελεστή επιβράδυνσης s. Kαι πράγματι, ένα νετρόνιο το οποίο κινείται με ταχύτητες πολύ κοντά στην ταχύτητα του φωτός c, έχοντας μέσο χρόνο ζωής όταν είναι ακίνητο περίπου 12 λεπτά πριν από τη διάσπασή του, μπορεί να αυξήσει το μέσο χρόνο ζωής του, λειτουργώντας ακριβώς σαν ένα ρολόι το οποίο τρέχει αργά και διέπεται από ασθενείς αλληλεπιδράσεις, όπως συμπεριφέρονται και τα μιόνια (διαβάστε σχετικά ΕΔΩ).
Επομένως, τώρα όλα συνδέονται μεταξύ τους. Αν η λέξη «πραγματικότητα» έχει οποιοδήποτε νόημα, τότε στην πραγματικότητα τα κινούμενα ρολόγια τρέχουν αργά και οι κινούμενες ράβδοι συστέλλονται. Από την άλλη, όμως, έχουμε φτάσει στο σημείο να είμαστε περισσότερο επιφυλακτικοί απέναντι στην αληθινή σημασία της λέξης «πραγματικός». Ο μηχανισμός ο οποίος δίνει την πραγματική εξήγηση ενός φαινομένου σε ένα σύστημα αναφοράς ενδέχεται να είναι εντελώς διαφορετικός από τον μηχανισμό που εξηγεί το φαινόμενο σε ένα άλλο σύστημα αναφοράς.
Σκεφτείτε το ακόλουθο παράδειγμα (διαβάστε επίσης εδώ, εδώ και εδώ): Έχουμε δυο πυραύλους, τους οποίους ενώνει ένα μακρύ, τεντωμένο σχοινί. Σε μία συγκεκριμένη χρονική στιγμή και οι δύο πύραυλοι αρχίζουν να κινούνται κατά μήκος της διεύθυνσης του σχοινιού, ας πούμε προς τα ανατολικά, με την ίδια ταχύτητα v. Επειδή οι πύραυλοι αρχίζουν να κινούνται την ίδια στιγμή και με την ίδια ταχύτητα η απόσταση μεταξύ τους δεν αλλάζει. Και επειδή διατηρούν την απόσταση ανάμεσά τους, η ανάγκη για το κινούμενο σχοινί να συσταλεί σταματά να υφίσταται, επομένως το σχοινί τεντώνεται σε μήκος πέρα από το κανονικό του μήκος στη νέα κινούμενη κατάστασή του. Αν οι πύραυλοι κινούνται αρκετά γρήγορα, αυτό το τέντωμα θα ξεπεράσει το ελαστικό όριο του σχοινιού και το σχοινί θα σπάσει. Το συγκεκριμένο παράδειγμα αποτελεί μία παραστατική εκδήλωση της πραγματικότητας της συστολής του μήκους.
Το παράδειγμα, όμως, ερμηνεύεται εντελώς διαφορετικά σε ένα σύστημα αναφοράς που κινείται κατά μήκος του σχοινιού με ταχύτητα v. Αρχικά και οι δυο πύραυλοι και το σχοινί – το οποίο έχει συσταλεί σε αυτό το σύστημα αναφοράς – κινούνται προς τα δυτικά με ταχύτητα v. Συνεπώς ο πύραυλος που βρίσκεται ανατολικά σταματά να κινείται, αλλά ο πύραυλος που βρίσκεται δυτικά συνεχίζει να κινείται για λίγο ακόμα πριν σταματήσει, γι αυτό το σχοινί τεντώνει και τελικά σπάει.
Η αλήθεια είναι ότι και οι δυο περιγραφές αποδεικνύονται αρκετά πιο περίπλοκες. Και αυτό γιατί η κίνηση που επιβάλλεται σε οποιαδήποτε άκρη του σχοινιού με την ταχύτητα των ελαστικών κυμάτων μέσα στο σχοινί, ταχύτητα η οποία είναι θεωρείται εξαιρετικά χαμηλή στην κλίμακα της ταχύτητας του φωτός, με αποτέλεσμα η πιο αναλυτική από τις δυο να περιλαμβάνει επίσης δυο διαφορετικές εκδοχές. Κάθε εκδοχή είναι απολυτως σωστή για το σύστημα αναφοράς στο οποίο αναφέρεται. Η ταυτόχρονη ισχύς και των δυο περιγραφών, σύμφωνα με το κατάλληλο σύστημα αναφοράς, δεν είναι περισσότερο – ή λιγότερο – παράξενη από την αίσθηση που έχουν οι κα΄τοικοι στη Νέα Υόρκη για τους κατοίκους του Σίδνεϋ όταν υποστηρίζουν ότι βρίσκονται ανάποδα σε σχέση με αυτούς, αλλά φυσικά και το αντίστροφο. Και οι δυο είναι στην ουσία διαφορετικοί τρόποι περιγραφής των ίδιων φαινομένων.
Ένα σημαντικό μάθημα που παίρνουμε από τη σχετικότητα είναι ότι τελικά υπάρχουν λιγότερα εγγενή στοιχεία στα πράγματα από όσα κάποτε πιστεύαμε. Πολλά από αυτά τα στοιχεία τα οποία τα οποία θεωρούσαμε ότι ήταν έμφυτα, τώρα αποδεικνύονται τελικά να είναι μέρος της σύμβασης που εμείς επιλέγουμε για την περιγραφή των φαινομένων. Αυτό δεν σημαίνει ότι δεν υπάρχει τίποτε έμφυτο σε αυτά τα φαινόμενα. Ότιδήποτε έχουμε διδαχθεί ως έμφυτο – όπως το διάστημα ανάμεσα σε δύο γεγονότα, για παράδειγμα – καταλήγει να θεωρείται παράξενο και άγνωστο, ενώ ότιδήποτε θεωρούσαμε κάποτε ως έμφυτο – όπως ο χρόνος ανάμεσα σε δυο γεγονότα – καταλήγει να είναι απλώς μέρος τη σύμβασης.
Η διαδικασία της συνειδητοποίησης ότι οι παλιές μας πεποιθήσεις δεν ευσταθούν πια, η οποία μας οδηγεί και στην επίπονη προσπάθεια να αναγνωρίσουμε και να συμβιβαστούμε με όλα τα λάθη του παρελθόντος, μας δίνει τη δυνατότητα να θεσπίσουμε στιβαρές και βελτιωμένες πεποιθήσεις οι οποίες θα αντικαταστήσουν τις παλιές. Και είναι ακριβώς αυτή η διαδικασία που κάνει συναρπαστική την αναζήτηση της επιστήμης. Ο κόσμος μας θεωρώ ότι θα ήταν πολύ καλύτερος για όλους μας αν αυτή η χαρά της αποκαθήλωσης των δικών μας στρεβλών πεποιθήσεων αποτελούσε πιο συχνό φαινόμενο και σε άλλους τομείς της ανθρώπινης δραστηριότητας.
πηγή: N. David Mermin «Είναι θέμα χρόνου», εκδόσεις ΡΟΠΗ.
Κατηγορίες:ΣΧΕΤΙΚΟΤΗΤΑ
Σχολιάστε