Αρχική › ΜΑΘΗΜΑΤΙΚΑ › Ατελείωτες τετραγωνικές ρίζες από τον Ραμανουτζάν

Ατελείωτες τετραγωνικές ρίζες από τον Ραμανουτζάν

By on • ( 0 )

Δυο σχόλια σχετικά με τα προβλήματα που παρουσιάζονται στην ανάρτηση με τίτλο «Τρεις μαθηματικοί γρίφοι του Ραμανουτζάν» .

(Ι) Όσον αφορά το πρώτο πρόβλημα που αναφέρεται στην απόδειξη της αριθμητικής σχέσης με τις ατελείωτες εγκιβωτισμένες τετραγωνικές ρίζες:
3=\sqrt{1+2\sqrt{1+3\sqrt{1 + 4\sqrt{1+5\sqrt{\cdots}}}}}
Πρόκειται για μια εφαρμογή της γενικότερης εξίσωσης που βρίσκεται στο πρώτο σημειωματάριο του Ραμανουτζάν. Σύμφωνα με το «θεώρημα» αυτό αν σπάσουμε οποιοδήποτε αριθμό σε τρία μέρη α, b και c, τότε ισχύει:
a + b + c = \sqrt{a c + (a+b)^2 +c \sqrt{a(b+c)+(a+b)^2 + (b+c) \sqrt{\cdots }}}
Έτσι, αν στην παραπάνω σχέση θέσουμε a=0, b=1, c=2 προκύπτει 3=\sqrt{1+2\sqrt{1+3\sqrt{1 + 4\sqrt{\cdots}}}}
ενώ θέτοντας a=1, b=1, c=1 προκύπτει 3=\sqrt{5+\sqrt{6+2\sqrt{7 + 3\sqrt{\cdots}}}} , ή π.χ. για a= b=1, c=2 παίρνουμε 4=\sqrt{6+2\sqrt{7+3\sqrt{8 + 4\sqrt{9 + \cdots}}}} κ.ο.κ

(ΙΙ) Το δεύτερο πρόβλημα, στην ίδια ανάρτηση, αναφέρεται στην εξίσωση που συσχετίζει την χρυσή αναλογία με ένα συνεχές κλάσμα:
\phi = \frac{1+\sqrt{5}}{2} = 1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\ddots }}}}
Μια ανάλογη εξίσωση, αλλά με συνεχείς τετραγωνικές ρίζες, είναι η εξής: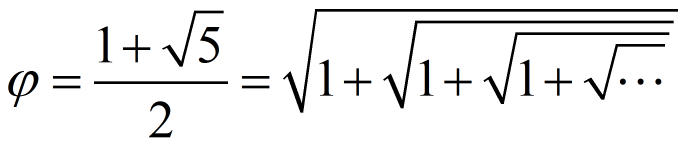phi4H απόδειξη γίνεται εύκολα, δεδομένου ότι η παράσταση στο κόκκινο πλαίσιο phi2ταυτίζεται με την αρχική, οπότε: \phi = \sqrt{1 + \phi} ή \phi^2 -\phi -1 =0 κ.λπ.

‹
›

Κατηγορίες:ΜΑΘΗΜΑΤΙΚΑ

Ετικέτες: ,

Σχολιάστε

Ο ιστότοπος χρησιμοποιεί το Akismet για την εξάλειψη των ανεπιθύμητων σχολίων. Μάθετε πως επεξεργάζονται τα δεδομένα των σχολίων σας.