Αρχική › ΜΑΘΗΜΑΤΙΚΑ › H προσέγγιση ενός δύσκολου ολοκληρώματος

H προσέγγιση ενός δύσκολου ολοκληρώματος

By on • ( 1 )

Το ζητούμενο είναι να βρεθεί μια προσέγγιση για ολοκληρώματα της μορφής:
I=\int\limits_{a}^{b} e^{-\frac{S(x)}{\epsilon}} dx  όταν η συνάρτηση S(x) παρουσιάζει ακρότατο και \epsilon \ll 1 .  Όπως θα δούμε, ολοκληρώματα αυτής της μορφής παίζουν σημαντικό ρόλο στη Φυσική.

Ας ξεκινήσουμε με μια συνάρτηση που παρουσιάζει ολικό ακρότατο
π.χ. την S(x) = -\frac{1}{1+(x-1)^{2}} και ένα έψιλον όχι τόσο πολύ μικρό \epsilon = 0.1
Τότε θέτοντας f(x) = \frac{S(x)}{\epsilon}
έχουμε
f(x) = -\frac{10}{1+(x-1)^{2}} της οποίας η γραφική παράσταση φαίνεται στο σχήμα:
plot
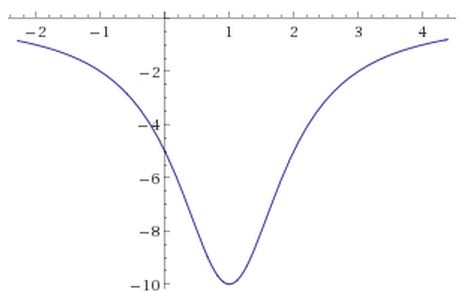
Παρατηρούμε ότι η συνάρτηση εμφανίζει ελάχιστο στο σημείο x_{0}=1 .
Πράγματι ισχύουν  f(x)\geqslant f(1)=-10 , f'(x)=0 \Rightarrow \frac{20(x-1)}{[(x-1)^2 + 1]^2}=0 \Rightarrow x=x_{0}=1
και f''(x_{0} = 1)=20>0 .

Το ολοκλήρωμα I=\int\limits_{a}^{b} e^{-\frac{S(x)}{\epsilon}} dx \equiv\int\limits_{a}^{b} e^{-f(x)} dx μπορεί να υπολογιστεί αριθμητικά.

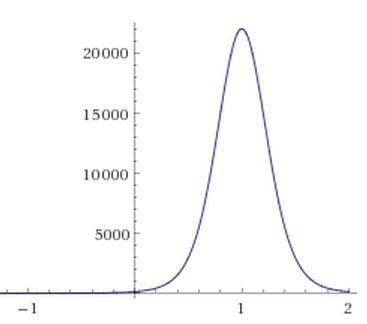
΄Το διάγραμμα της προς ολοκλήρωση συνάρτησης

Το διάγραμμα της προς ολοκλήρωση συνάρτησης exp[-f(x)] μοιάζει πολύ με την γκαουσιανή συνάρτηση. Το γεγονός αυτό παίζει σημαντικό ρόλο στην προσέγγιση του ολοκληρώματος. 

Για παράδειγμα χρησιμοποιώντας το πρόγραμμα mathematica παίρνουμε
I=\int\limits_{-5}^{10} e^{-f(x)} dx = \int\limits_{-5}^{10} e^{\frac{10}{1+(x-1)^{2}}} dx = 13553,2
(τα όρια ολοκλήρωσης μπήκαν στην τύχη)

Τα ολοκληρώματα αυτής της μορφής μπορούν να προσεγγιστούν και χωρίς αριθμητική ολοκλήρωση, από την απλούστατη σχέση:
I=\int_{a}^{b} e^{-\frac{S(x)}{\epsilon}} dx \approx e^{-\frac{S(x_{0})}{\epsilon}} \sqrt{\frac{2 \pi \epsilon}{S''(x_{0})}}
αρκεί \epsilon \ll 1 και η συνάρτηση S(x) να παρουσιάζει ολικό ελάχιστο στο σημείο x=x_{0} .
Για τη συνάρτηση του προηγούμενου παραδείγματος έχουμε S(x_{0}=1) = -1 , S''(1) =2 και για \epsilon = 0.1 , προκύπτει:
I \approx e^{-\frac{S(x_{0})}{\epsilon}} \sqrt{\frac{2 \pi \epsilon}{S''(x_{0})}} = 12345,8
που διαφέρει από την τιμή που δίνει το mathematica κατά 8,9%.
Όμως η τιμή του έψιλον που επιλέχθηκε δεν ήταν πολύ μικρή. Έτσι, καθώς το \epsilon \rightarrow 0 , η προσέγγιση γίνεται πολύ καλύτερη.

Απόδειξη της προσέγγισης:  I=\int_{a}^{b} e^{-\frac{S(x)}{\epsilon}} dx \approx e^{-\frac{S(x_{0})}{\epsilon}} \sqrt{\frac{2 \pi \epsilon}{S''(x_{0})}}

Αναπτύσσουμε κατά Taylor την S(x)
S(x) = S(x_{0}) + S'(x_{0}) \frac{(x-x_{0})}{1!} + S''(x_{0}) \frac{(x-x_{0})^{2}}{2!} + \cdots
Εφόσον η S(x) έχει ακρότατο στο x=x0 θα ισχύει S'(x0)=0, οπότε
S(x) \cong S(x_{0}) + S''(x_{0}) \frac{(x-x_{0})^{2}}{2!}
Aντικαθιστώντας στο ολοκλήρωμα παίρνουμε
I=\int_{a}^{b} e^{-\frac{S(x)}{\epsilon}} dx \approx e^{-\frac{S(x_{0})}{\epsilon}} \int_{a}^{b} e^{-S''(x_{0}) \frac{(x-x_{0})^2}{2 \epsilon}} dx
Καθώς \epsilon \rightarrow 0 το ορισμένο ολοκλήρωμα με την κατάλληλη αλλαγή μεταβλητής υπολογίζεται όπως το ολοκλήρωμα της γκαουσιανής συνάρτησης: \int\limits_{-\infty}^{\infty} e^{-u^{2}} du = \sqrt{\pi} , δίνοντας έτσι την ζητούμενη προσέγγιση.
Στη βιβλιογραφία η παραπάνω μέθοδος αναφέρεται ως μέθοδος Laplace.

Η απάντηση στο ερώτημα «τι σχέση έχουν όλα τα παραπάνω με τη Φυσική;» θα δοθεί σε μια άλλη ανάρτηση.

‹
›

Κατηγορίες:ΜΑΘΗΜΑΤΙΚΑ

Ετικέτες: ,

1 reply

  1. thanos713's avatar
    thanos713
    27/05/2013 • 4:08 μμ

    Περιμένουμε την σχέση με την Φυσική!

    Reply ↓

Σχολιάστε

Ο ιστότοπος χρησιμοποιεί το Akismet για την εξάλειψη των ανεπιθύμητων σχολίων. Μάθετε πως επεξεργάζονται τα δεδομένα των σχολίων σας.